cac dang bai tap ham so y ax2 a khac 0 phuong trinh bac hai mot an
108
3
0
THÔNG TIN TÀI LIỆU
Thông tin cơ bản
| Tiêu đề | Hàm Số Y = Ax2, A Khác 0. Phương Trình Bậc Hai Một Ẩn |
|---|
| Định dạng | |
|---|---|
| Số trang | 108 |
| Dung lượng | 1,03 MB |
Nội dung
Ngày đăng: 04/12/2022, 08:29
HÌNH ẢNH LIÊN QUAN

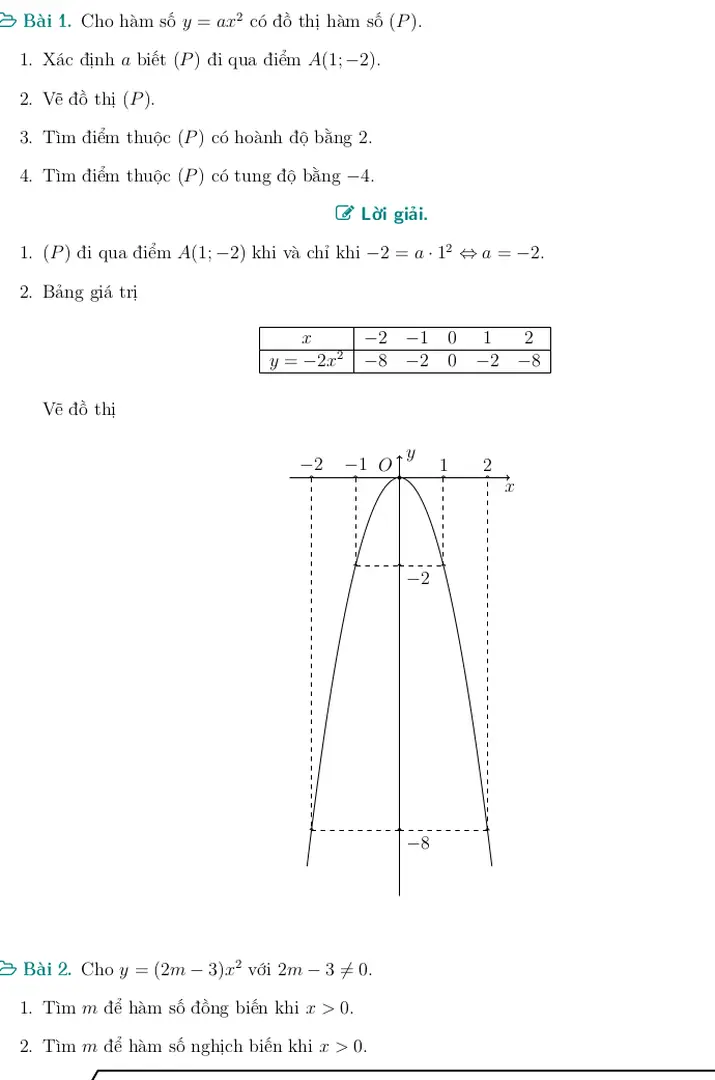







TÀI LIỆU CÙNG NGƯỜI DÙNG
-
69 5 0
-
6 4 0
-
4 1 0
-
3 2 0
-
4 3 0
-
3 2 0
TÀI LIỆU LIÊN QUAN
-
14 1,8K 28
-
4 5 0
-
41 5 0
-
137 712 0
-
20 16 0
-
39 72 0
-
51 38 0
-
15 120 0