cac bai toan chon loc trong he toa do oxyz phan 1 nguyen xuan chung
153
10
0
THÔNG TIN TÀI LIỆU
Thông tin cơ bản
| Tiêu đề | Các Bài Toán Chọn Lọc Trong Hệ Tọa Độ Oxyz Phần 1 |
|---|---|
| Tác giả | Nguyen Xuan Chung |
| Trường học | Trường Đại Học |
| Thể loại | Tài Liệu Học Tập |
| Định dạng | |
|---|---|
| Số trang | 153 |
| Dung lượng | 6,94 MB |
Nội dung
Ngày đăng: 13/10/2022, 07:18
HÌNH ẢNH LIÊN QUAN









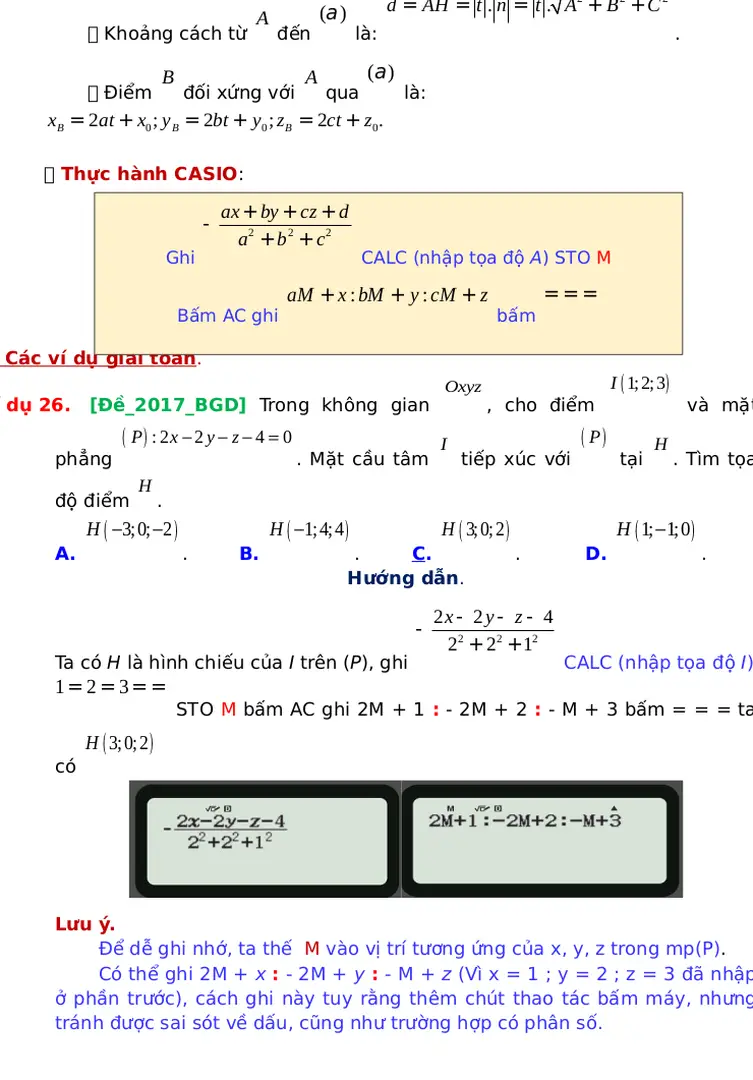



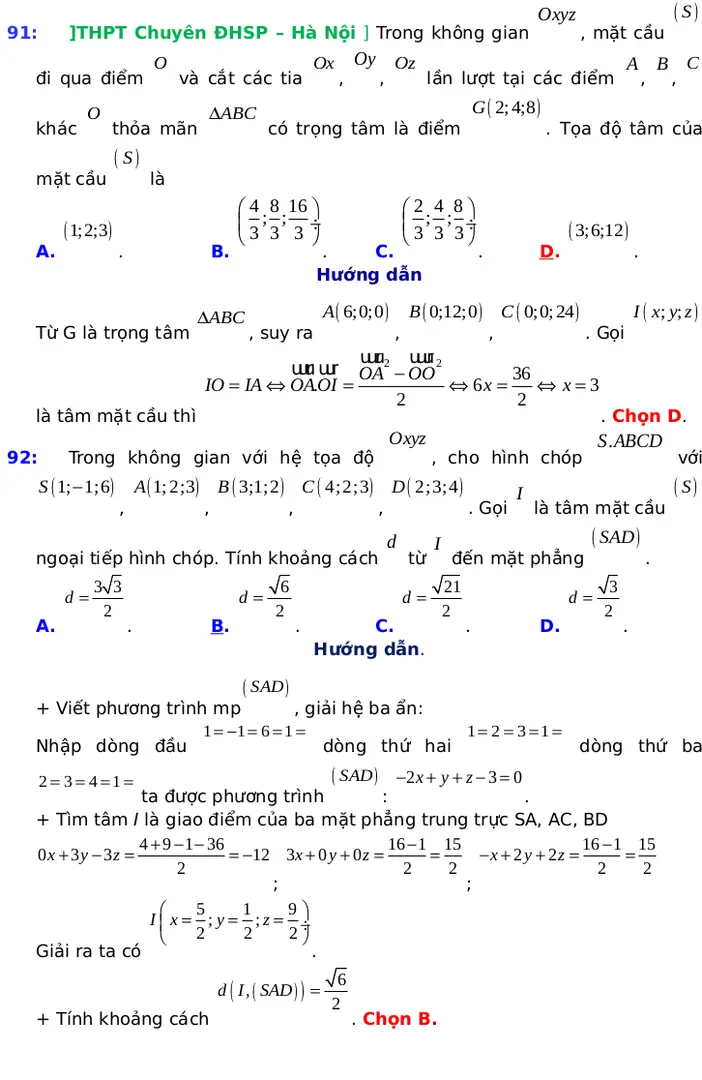

TÀI LIỆU CÙNG NGƯỜI DÙNG
-
4 2 0
-
1 0 0
-
13 1 0
-
55 1 0
-
5 4 0
-
10 1 0
TÀI LIỆU LIÊN QUAN
-
153 10 0
-
112 7 0
-
8 4 0
-
26 4 0
-
9 8 0
-
2 23 0
-
2 13 0
-
20 8 0