GIỚ I THI Ệ U CHUNG
Lý do ch ọn đề tài
Các bài toán tối ưu tổ hợp đóng vai trò quan trọng trong nhiều lĩnh vực như công nghệ thông tin, sản xuất, kinh tế và quốc phòng Một số bài toán kinh điển bao gồm bài toán người du lịch (TSP), bài toán n-queens, và bài toán tô màu đồ thị Việc giải quyết hiệu quả những bài toán này không chỉ giúp tối ưu hóa lịch trình làm việc, giảm thiểu xung đột, mà còn nâng cao hiệu suất thiết bị và giảm chi phí sản xuất Điều này góp phần cải thiện chất lượng cuộc sống và mang lại lợi ích cho người tiêu dùng Tầm quan trọng của các bài toán tối ưu tổ hợp trong cuộc sống hàng ngày là không thể phủ nhận.
Bài toán lập lịch thi đấu thể thao (TTP) là một bài toán tối ưu tổ hợp, nhưng khi kích thước bài toán tăng lên, không gian tìm kiếm trở nên phức tạp và bùng nổ, khiến các phương pháp tìm kiếm thông thường không còn hiệu quả Tìm kiếm cục bộ được phát triển để giải quyết vấn đề này, cho phép tìm kiếm các trạng thái tốt trong thời gian hợp lý Tuy nhiên, phương pháp này vẫn gặp phải những hạn chế, như thời gian tìm kiếm dài khi không gian tìm kiếm quá lớn, không thể đảm bảo tìm ra giải pháp tối ưu và dễ dẫn đến tình trạng bế tắc hoặc tối ưu cục bộ, đặc biệt khi có nhiều ràng buộc phức tạp.
Để đối phó với những thách thức trong việc lập lịch thi đấu thể thao dựa trên các ràng buộc, việc áp dụng các giải pháp như tìm kiếm tabu có thể giúp tìm ra giải pháp tối ưu trong thời gian hợp lý.
Trong luận văn này, chúng tôi nghiên cứu bài toán "Lập lịch thi đấu thể thao" (TTP) thông qua các phương pháp xử lý dựa trên ràng buộc và kỹ thuật metaheuristic Simulated Annealing Mục tiêu là đánh giá mối tương quan giữa các giải pháp cho bài toán này.
M ụ c tiêu nghiên c ứ u
• Tìm hiểu các giải thuật tìm kiếm cục bộ dựa trên ràng buộc giải bài toán TTP
• Nghiên cứu giải thuật Simulated Annealing (SA) giải bài toán TTP
• Đánh giá được hiệu quả của giải thuật khi thay đổi các tham số, đưa ra hướng phát triển trong tương lai.
Đối tượ ng và ph ạ m vi nghiên c ứ u
Nghiên cứu lý thuyết và kỹ thuật giải toán trong Quy hoạch ràng buộc và Tìm kiếm cục bộ, nhằm áp dụng vào bài toán lập lịch thi đấu thể thao, giúp đánh giá hiệu quả của từng phương pháp.
Hướ ng nghiên c ứ u c ủa đề tài
• Tìm hiểu các thuật toán tìm kiếm cục bộ cho bài toán TTP
• Tìm hiểu các công cụ giải bài toán TTP dựa trên ràng buộc
Thuật toán Simulated Annealing (SA) được áp dụng để giải quyết bài toán TTP, đồng thời tiến hành đánh giá và so sánh hiệu quả của phương pháp này với việc sử dụng Lập trình Ràng buộc (Constraint Programming - CP) trong việc giải TTP.
Phương pháp nghiên cứ u
• Tìm hiểu bài toán TTP và các biến thể của nó được các nhà khoa học đề xuất và nghiên cứu
• Nghiên cứu tài liệu khoa học vềcác phương pháp tìm kiếm cục bộ
• Tìm hiểu, sử dụng các công cụ giải bài toán bằng kĩ thuật quy hoạch ràng buộc
• Nghiên cứu các tài liệu khoa học về giải bài toán TTP
• Sử dụng thuật toán SA cài đặt giải bài toán TTP
• Đánh giá hiệu quả việc áp dụng thuật toán SA so với sử dụng công cụ OR-Tools giải bài toán TTP.
Ý nghĩa khoa họ c c ủa đề bài
Nghiên cứu về việc áp dụng thuật toán SA trong giải quyết bài toán TTP và sử dụng công cụ OR-Tools với quy hoạch ràng buộc giúp kiểm chứng và so sánh hiệu quả của các phương pháp này Kết quả thực nghiệm sẽ cho phép lựa chọn hướng giải quyết tối ưu hơn, từ đó có thể kết hợp với các phương pháp khác trong việc giải bài toán TTP trong tương lai.
N ộ i dung bài lu ận văn
Chương 2: Cơ sở lý thuyết
Chương 3: Các phương pháp giải bài toán lập lịch thi đấu thể thao
Chương 4: Kết quả thực nghiệm
CƠ SỞ LÝ THUY Ế T
Bài toán t ối ưu tổ h ợ p
TTP thuộc lớp bài toán tối ưu tổ hợp, do đó trong phần này, chúng tôi sẽ trình bày các định nghĩa và khái niệm cần thiết để giải quyết bài toán tối ưu tổ hợp nói chung, cũng như bài toán TTP một cách cụ thể.
Bài toán tối ưu hóa tổ hợp (Combinatorial Optimization) liên quan đến việc tìm giá trị cho các biến số rời rạc nhằm đạt được lời giải tối ưu, đồng thời xem xét hàm đánh giá đã cho Bài toán này có thể là tìm cực đại hoặc cực tiểu Thông thường, bài toán tối ưu hóa tổ hợp được biểu diễn dưới dạng bộ ba (S, f, Ω).
• S là tập các lời giải ứng cử viên.
• F là hàm đánh giá (hàm này gán giá trị f(s) sao cho mỗi lời giải ứng viên s ∈ S)
• Ω là tập các ràng buộc của bài toán
Các lời giải thuộc tập S * ⸦ S thỏa mãn ràng buộc Ω được gọi là lời giải khả thi Mục tiêu của bài toán là tìm ra lời giải s * với chi phí nhỏ nhất, tức là f(s *) < f(s) với mọi s ∈ S Ngược lại, bài toán tối ưu hóa cực đại sẽ có những yêu cầu khác.
Tối ưu hóa tổ hợp là một lĩnh vực quan trọng với nhiều ứng dụng thực tiễn Một số bài toán kinh điển trong lĩnh vực này bao gồm bài toán người du lịch, bài toán n-queens, bài toán tô màu đồ thị và bài toán xếp lịch y tá.
Những khái niệm quan trọng trong một bài toán tối ưu tổ hợp:
• Biến quyết định (Decision variable)
Biến quyết định trong bài toán tối ưu hóa tổ hợp là yếu tố mà người ra quyết định có thể kiểm soát và cần xác định giá trị của nó để đạt được mục tiêu tối ưu.
• Miền xác định của biến quyết định (Domain)
Miền giá trị của các biến quyết định là tập hợp tất cả các giá trị có thể gán cho biến đó.
Một ràng buộc của bài toán tối ưu hóa tổ hợp là một điều kiện mà một tập các biến quyết định của bài toán cần thỏa mãn
• Hàm mục tiêu của bài toán (Object function)
Hàm mục tiêu trong bài toán tối ưu hóa tổ hợp là một hàm được xác định trên một tập hợp các biến quyết định, với mục tiêu là tối ưu hóa nó bằng cách cực đại hóa hoặc cực tiểu hóa giá trị của hàm.
• Lời giải của bài toán (Solution)
Một lời giải của bài toán tối ưu hóa tổ hợp là một bộ giá trịxác định gán cho tập các biến quyết định của bài toán
• Lời giải chấp nhận được (Feasible Solution)
Một lời giải chấp nhận được của bài toán tối ưu tổ hợp là một lời giải thỏa mãn mọi ràng buộc của bài toán
• Ví dụ1: Bài toán người bán hàng (TSP):
Một người giao hàng cần thực hiện chuyến giao hàng tại n thành phố, bắt đầu từ một thành phố cụ thể, đi qua các thành phố khác và quay trở về thành phố ban đầu Mỗi thành phố chỉ được ghé thăm một lần, và khoảng cách giữa các thành phố đã được xác định trước Nhiệm vụ là tìm một lộ trình khép kín sao cho tổng quãng đường di chuyển của người giao hàng là ngắn nhất.
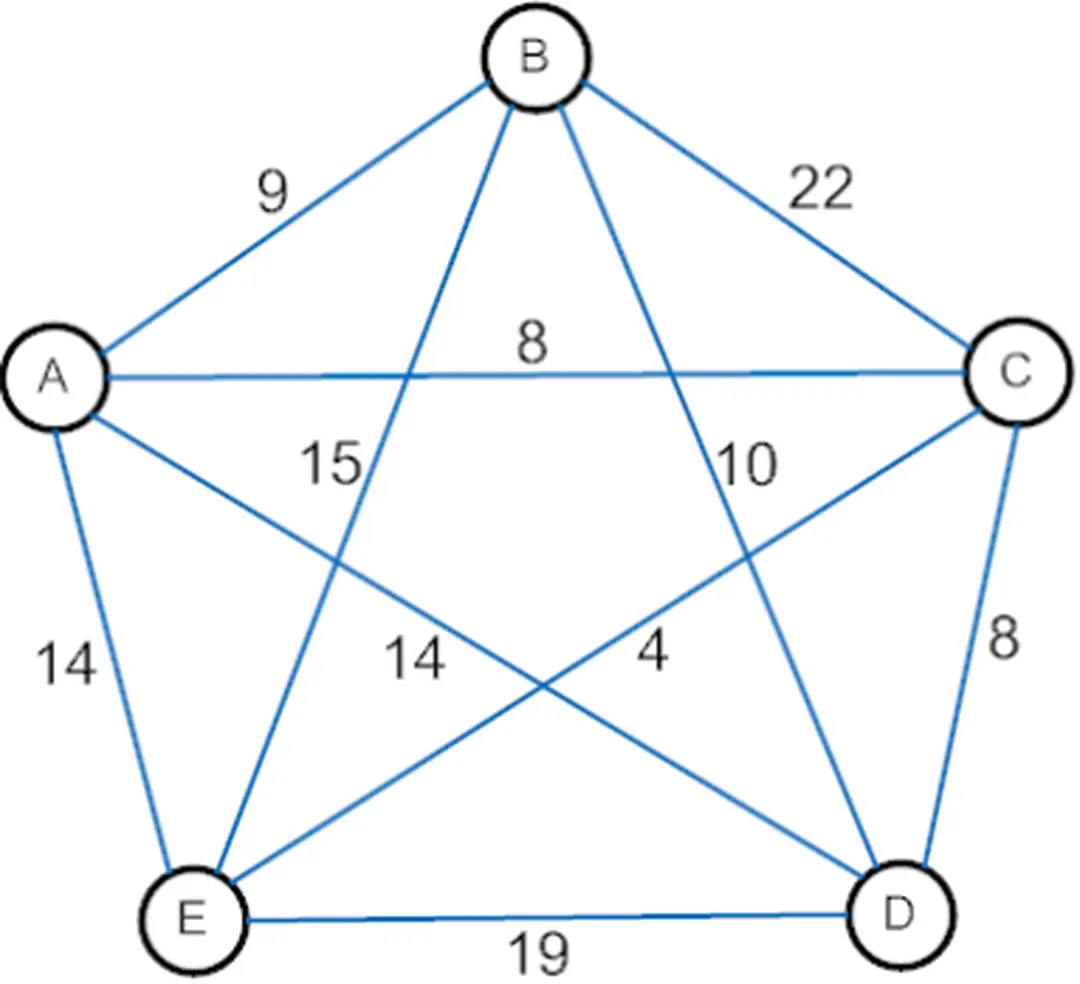
Bài toán TSP (Traveling Salesman Problem) được mô tả trên đồ thị vô hướng có trọng số G = (V, E), trong đó mỗi thành phố là một đỉnh và cạnh nối hai đỉnh thể hiện khoảng cách giữa các thành phố Mục tiêu của bài toán là tìm một chu trình Hamilton, tức là chu trình đi qua tất cả các đỉnh đúng một lần, với tổng độ dài các cạnh là nhỏ nhất.
Hình 2.1 Bài toán TSP biểu diễn dưới dạng đồ thị
• n là số thành phốmà người bán hàng cần phải đi qua
• D là ma trận khoảng cách (n, n) giữa các thành phố
• Chu trình di chuyển của người bán hàng và tổng quãng đường di chuyển nhỏ nhất
Bài toán TSP (Traveling Salesman Problem) là một trong những bài toán NP-khó, với nhiều phương pháp tiếp cận khác nhau Thuật toán tìm kiếm lời giải tối ưu thường hiệu quả cho các bài toán nhỏ, trong khi thuật toán heuristic giúp tìm ra những giải pháp tốt nhưng không nhất thiết phải tối ưu Ngoài ra, thuật toán xấp xỉ được thiết kế để cung cấp giải pháp gần tối ưu Một số thuật toán phổ biến bao gồm phương pháp vét cạn, kỹ thuật tham ăn và giải thuật nhánh cận Bài toán TSP có ứng dụng rộng rãi trong thực tế, đặc biệt trong lĩnh vực giao vận của shipper, vận tải hàng hóa giữa các thành phố, cũng như trong các quy trình sản xuất của nhà máy và xí nghiệp.
• Ví dụ 2: Bài toán phân công giảng dạy (BCA):
Trong một ngôi trường có M giáo viên và N môn học, mỗi môn học cần được phân công cho một giáo viên duy nhất Các giáo viên chỉ có thể dạy những môn học nhất định dựa trên khả năng chuyên môn của họ, được thể hiện qua tập C(i) Mỗi môn học i có số tiết t(i) và có một tập S chứa các cặp môn học không thể phân công cho cùng một giáo viên do xung đột thời gian Ràng buộc của bài toán yêu cầu tổng số tiết của mỗi giáo viên phải nằm trong khoảng từ α đến β Mục tiêu là xây dựng lịch phân công sao cho số tiết nhiều nhất của giáo viên không được vượt quá mức tối thiểu.
• M là sốgiáo viên trong trường
• N là số môn cần được giảng dạy
• C là danh sách số môn học có thể dạy bởi các giáo viên
• t là danh sách tiết học của các môn
• S là danh sách các cặp môn học trùng tiết
• Hằng số α, β để ràng buộc số tiết học được phân công cho từng giáo viên
• Chu trình di chuyển của người bán hàng và tổng quãng đường di chuyển nhỏ nhất
Bài toán BCA là một ví dụ điển hình về lập lịch với nhiều ràng buộc Để giải quyết vấn đề này, có nhiều phương pháp tiếp cận khác nhau, trong đó quy hoạch ràng buộc là một trong những phương pháp hiệu quả, với mô hình ràng buộc được mô tả chi tiết dưới đây.
• MH_GV[][]: Tập hợp các môn học mà từng giáo viên được dạy
• T_MH: Tập hợp số tiết của các môn học
• Cặp I, J là đôi một là các cặp môn học tiên quyết
Biến quyết định trong model:
• x[i][j] = {0, 1} Với i ∈ N, j ∈ 𝑀𝑀: Quy định giáo viên i dạy môn j
• y[j][i] = {0,1} Với i ∈ M, j ∈ 𝑁𝑁 Đảm nhận vịtrí trung gian để xây dựng các ràng buộc
• maxT: Là biến ràng buộc hàm mục tiêu của bài toán
Bài toán BCA rất hữu ích trong việc phân công công việc và giảng dạy cho các tổ chức như công ty, trường học, cũng như trong việc lập lịch làm việc cho các hệ thống máy móc trong quy trình sản xuất công nghiệp.
Ngoài các ví dụ đã nêu, bài toán tối ưu tổ hợp xuất hiện nhiều trong cuộc sống hàng ngày Nghiên cứu và giải quyết những bài toán này đóng vai trò quan trọng trong việc cải thiện hiệu quả và tối ưu hóa các quy trình.
8 ưu tổ hợp là công việc vô cùng ý nghĩa và có tác động tích cực đến sự phát triển của nền văn minh hiện đại.
Bài toán l ậ p l ịch thi đấ u th ể thao
TTP là bài toán lập lịch thi đấu cho các đội trong một giải đấu vòng tròn, nhằm tối ưu hóa việc di chuyển của các đội Bài toán này được giới thiệu trong nghiên cứu "The Traveling Tournament."
Bài viết "Problem Description and Benchmarks" của các tác giả Kelly Easton, George Nemhauser, Michael A Trick, xuất bản vào ngày 01/01/2001, nêu bật rằng việc tìm ra kết quả tối ưu cho bài toán TTP (Traveling Tournament Problem) là rất khó khăn, ngay cả với số đội nhỏ Điều này tạo ra thách thức cho các kỹ thuật lập trình giải nguyên tuyến tính và giải ràng buộc TTP thuộc lớp bài toán NP-khó, với không gian tìm kiếm mở rộng khi n tăng, và hiện chưa có lời giải chính xác trong thời gian đa thức Bài toán này vẫn là đề tài nghiên cứu quan trọng trong lĩnh vực tối ưu hóa tổ hợp, nhờ vào những thách thức và ứng dụng mà nó mang lại Các kết quả cải tiến đang được liên tục cập nhật và tổng hợp.
Phát biểu bài toán TTP bằng lời:
Trong giải đấu này, mỗi đội sẽ tham gia thi đấu với n-1 đội còn lại theo thể thức lượt đi lượt về, nghĩa là mỗi đội sẽ có cơ hội đối đầu với tất cả các đội khác trong giải.
Giải đấu sẽ diễn ra với 2 trận đấu cho mỗi đội, bao gồm 1 trận trên sân nhà và 1 trận trên sân khách Mỗi tuần sẽ có n/2 trận đấu được tổ chức, dẫn đến tổng cộng 2(n-1) trận trong suốt giải Khoảng cách giữa các điểm thi đấu được thể hiện qua ma trận khoảng cách (n, n) Mục tiêu chính của bài toán là giảm thiểu tổng chi phí di chuyển của tất cả các đội trong giải đấu.
Bài toán yêu cầu rằng hai đội không được thi đấu với nhau trong hai tuần liên tiếp và không được thi đấu trên sân nhà hoặc sân khách quá ba tuần liên tiếp.
Ngoài những ràng buộc cơ bản, bài toán còn có một số biến thể được đề cập và nghiên cứu hiện nay như sau:
Nhân bản (Mirrored): Là một giải đấu mà phải có một lịch đấu vòng tròn ở n-1 lượt trận đầu tiên và lặp lại lịch trình đó ở n-1 lượt đấu còn lại
Không lặp (No Repeaters): Không có những đội i, j nào mà đội i đấu với đội j và sau đó đội j lại đấu với đội i ở lượt đấu kế tiếp
Bài toán TTP hiện nay vẫn chưa có lời giải chính xác với n = 6 trở lên
• n, sốđội tham gia giải đấu, n luôn chẵn
• D là ma trận khoảng cách (n, n)
• L, U lần lượt là tham số chặn dưới và chặn trên của việc thi đấu liên tục trên sân nhà (sân khách)
• Các lượt thi đấu liên tục trên sân nhà (sân khách) nằm trong khoảng L và U
• Tổng quãng đường di chuyển của các đội là nhỏ nhất
Chúng tôi tập trung nghiên cứu bài toán cơ sở TTP với các ràng buộc gốc, mở rộng với nhiều biến thể nhưng hạn chế tối đa số ràng buộc chặt nhằm giảm thiểu độ phức tạp của bài toán.
2.2.1 Yêu cầu của bài toán
Trong mùa giải, mỗi cặp đội sẽ gặp nhau hai lần, bao gồm một trận đấu trên sân nhà và một trận trên sân khách Mục tiêu chính của bài toán là tối ưu hóa tổng quãng đường di chuyển của các đội sao cho ngắn nhất có thể.
2.2.2 Dạng dữ liệu đầu vào của bài toán
Dữ liệu đầu vào của bài toán sẽ là một ma trận khoảng cách giữa các sân vận động của các đội tham gia trong giải đấu
Ví dụ: 1 mẫu dữ liệu
Hình 2.3 Mẫu dữ liệu cho kích thước bài toán 4 đội (n=4)
Lý thuy ế t v ề quy ho ạ ch ràng bu ộ c và tìm ki ế m c ụ c b ộ
Bài toán tối ưu tổ hợp có nhiều phương pháp giải khác nhau, mỗi phương pháp phục vụ cho những mục tiêu riêng như tối ưu giá trị hàm mục tiêu và giảm thời gian tìm kiếm kết quả chấp nhận được Đối với bài toán TTP, chúng tôi áp dụng hai phương pháp chính: Quy hoạch ràng buộc và Tìm kiếm cục bộ thông qua thuật toán Simulated Annealing.
2.3.1 Phương pháp quy hoạch ràng buộc
Quy hoạch ràng buộc (Constraint Programming - CP) là một phương pháp hiệu quả trong giải quyết các bài toán tối ưu tổ hợp, kết hợp giữa vận trù học, khoa học máy tính và trí tuệ nhân tạo CP được áp dụng rộng rãi trong các lĩnh vực như lập lịch, lập thời khoá biểu, lập tuyến điều hành xe và phân công ca trực Phương pháp này chủ yếu dựa vào hai thành phần chính: tỉa không gian tìm kiếm và phân nhánh Tỉa không gian tìm kiếm sử dụng các ràng buộc của bài toán để loại bỏ các giá trị không thỏa mãn, trong khi phân nhánh phân chia miền không gian tìm kiếm thành nhiều phần, cho phép áp dụng các chiến lược khác nhau tùy theo mô hình bài toán Việc phân nhánh thường bao gồm việc thử lần lượt từng giá trị còn lại trong miền giá trị của một biến và gán giá trị cho biến đó.
B Định nghĩa bài toán thỏa mãn ràng buộc
10 Định nghĩa về bài toán thỏa mãn ràng buộc (CSP) như sau Một bài toán CSP gồm 3 thành phần (X, D, C) với:
Hình 2.4 Ví dụ bài toán thỏa mãn ràng buộc
• X là bộ biến quyết định (Variables) gồm n phần tử: X = (X1, X2,…, Xn)
• D là miền giá trị (Domans): D = (D1, D2, …, Dn) là tập các giá trị mà biến quyết định X có thể nhận
• C là ràng buộc (Constraints) Tập hợp tất cả các ràng buộc
• f: Một số bài toán sẽ có hàm mục tiêu này để tối ưu theo yêu cầu đề bài
C Dùng ràng buộc để tỉa không gian tìm kiếm
Loại bỏ các giá trị thừa trong miền giá trị của biến giúp chuyển đổi bài toán thành một bài toán thoả mãn ràng buộc với miền giá trị nhỏ hơn Việc đạt được ràng buộc tổng thể thường khó khăn và tốn thời gian tính toán lớn, vì vậy các kỹ thuật tỉa được áp dụng cho từng ràng buộc một cách cục bộ Một trong những kỹ thuật tỉa hiệu quả là đảm bảo toàn vẹn miền giá trị (Domain Consistent - DC).
Trong bài toán thỏa mãn ràng buộc (CSP) được định nghĩa bởi bộ ba (X, D, C), một ràng buộc c ∈ C được xem là nhất quán với miền (domain consistent) nếu với mỗi biến Xi ∈ X(c) và mỗi giá trị v ∈ D(Xi), tồn tại một bộ giá trị cho các biến trong X(c) \ {Xi} sao cho ràng buộc c được thỏa mãn Bài toán CSP được coi là nhất quán với miền nếu mọi ràng buộc c ∈ C đều đạt tính chất này.
Ví dụ: CSP = (X, D, C) trong đó:
CSP này là domain consistent
Khi phân nhánh, xét X1 = 1, thuật toán DC sẽđưa CSP đã cho về CSP 1 tương đương các domain consistent với miền giá trịđược thu hẹp như sau: D 1 (X1) {1}, D 1 (X2) = {4,5,6,7}, D 1 (X3) = {2,3,4}, D 1 (X4) = {1,2,3,4,5}
Ví dụ: CSP = (X, D, C) trong đó:
CSP này rõ ràng là nhất quán về miền nhưng không tồn tại lời giải thỏa mãn các ràng buộc Phương pháp kiểm tra toàn vẹn tiến (Forward Checking - FC) được áp dụng để xác định tính khả thi của các lời giải.
Kỹ thuật toàn vẹn FC loại bỏ được ít giá trị không hợp lệ hơn nên kỹ thuật này yếu hơn kỹ thuật DC
Một ràng buộc c ∈ C được xem là toàn vẹn FC khi có nhiều hơn một biến chưa được gán giá trị, hoặc chỉ một biến chưa được gán giá trị nhưng c vẫn đảm bảo tính toàn vẹn miền giá trị.
Ví dụ: CSP = (X, D, C) trong đó:
CSP này là domain consistent
D 4 (X4) = {1, 2, 3, 4, 5, 6} N 1 = (X, D 1 , C) là toàn vẹn FC vì giá trị 6 trong miền giá trị của x4 không thỏa mãn ràng buộc của c2 iii Thuật toán Arc consistency (AC)
Hình 2.5 Mã giả thuật toán Arc Consistency
Thuật toán AC3(X,D,C) sử dụng một hàng đợi Q chứa tất cả các cặp (x,c), trong đó c là ràng buộc thuộc tập C và x là biến trong ràng buộc c Thuật toán lặp qua các cặp (x,c) trong Q và gọi hàm Revise(x,c) Nếu D(x) rỗng, thuật toán trả về false; nếu D(x) được sửa đổi, thì sẽ có một biến khác x’ thỏa mãn ràng buộc c’ Tất cả các cặp (x’,c’) sau đó được đưa lại vào hàng đợi Q Khi Q rỗng, thuật toán trả về true, đảm bảo rằng tất cả các miền đã được sửa đổi và các giá trị còn lại của tất cả các biến đều thỏa mãn mọi ràng buộc Hàm ReviseAC3(x,c) thực hiện việc tỉa các giá trị không phù hợp của x dựa vào ràng buộc c, kiểm tra từng giá trị v trong D(x) để xác định sự thỏa mãn các ràng buộc Nếu v không thỏa mãn, nó sẽ bị loại khỏi D(x) và miền giá trị D(x) sẽ thay đổi Hàm trả về true nếu miền D(x) được rút gọn, ngược lại trả về false.
D Phân nhánh và tìm kiếm quay lui
Phương pháp tỉa không gian tìm kiếm có nhược điểm là không đảm bảo tìm ra lời giải thỏa mãn tất cả các ràng buộc Vì vậy, cần kết hợp phương pháp này với tìm kiếm quay lui để nâng cao hiệu quả tìm kiếm.
Quay lui là một kỹ thuật tìm kiếm lời giải thường được sử dụng trong các bài toán thỏa mãn ràng buộc dựa trên đệ quy Phương pháp này thực hiện tìm kiếm từng bước, chọn lựa các phương án phù hợp với ràng buộc và tiến hành đệ quy Kỹ thuật này được phát triển bởi nhà toán học D H Lehmer vào những năm 1950.
Kỹ thuật tìm kiếm này dựa trên việc duyệt qua tất cả các khả năng trong không gian nghiệm cho đến khi tìm ra lời giải đúng, được gọi là tìm kiếm theo độ sâu (Depth-First Search) Trong quá trình tìm kiếm, nếu gặp điểm thỏa mãn, chương trình sẽ tiếp tục thực hiện đệ quy để khám phá các khả năng khác Ngược lại, nếu gặp điểm không thỏa mãn, chương trình sẽ quay lại điểm thỏa mãn trước đó và thử nghiệm các trường hợp khác Quá trình tìm kiếm sẽ kết thúc khi không còn lựa chọn nào khả thi.
Quá trình tìm kiếm được thực hiện thông qua một hàm đệ quy, trong đó mỗi lần gọi đệ quy sẽ lựa chọn một biến và gán tất cả các giá trị khả thi cho biến đó Sau đó, hàm lại tiếp tục gọi đệ quy để tìm giá trị cho các biến tiếp theo Kỹ thuật quy lui, so với tìm kiếm theo độ sâu, tiêu tốn ít bộ nhớ hơn vì chỉ lưu trữ trạng thái của một lời giải hiện tại và cập nhật nó.
Quay lui sử dụng một số thủ thuật để tăng tốc quá trình tìm kiếm, bao gồm việc xóa giá trị đã gán khỏi không gian tìm kiếm của các biến chưa được gán (kiểm tra tiến - forward checking) và kiểm tra các giá trị khác để phát hiện các giá trị vi phạm ràng buộc (lan truyền ràng buộc - constraint propagation).
Chia không gian tìm kiếm thành các không gian con Có một số chiến lược chia không gian tìm kiếm như sau:
• Liệt kê các giá trị cho biến được lựa chọn
• Phân hoạch tập giá trị của mỗi biến được lựa chọn thành 2 hoặc nhiều tập con
Việc tỉa không gian tìm kiếm (Propagation) một mình không đủ để tìm ra lời giải tối ưu đáp ứng các ràng buộc Do đó, cần kết hợp tỉa không gian tìm kiếm với phương pháp phân nhánh và tìm kiếm quay lui để đạt hiệu quả cao hơn trong việc tìm kiếm giải pháp.
Phân ra bài toán CSP P 0 ban đầu thành các CSP P 1,…, P M
• Tập các lời giải của P0 bằng hợp của tập các lời giải của P1,…,PM
• Miền giá trị mỗi biến trong P1, …, PM không lớn hơn miền giá trị P0
Cây tìm kiếm (Search Tree):
• Nút gốc của CSP P0ban đầu
• Mỗi nút của cây là 1 CSP
• Nếu P1, …, PM là các nút con của P0 thì tập các lời giài của P0 sẽ bằng với hợp của tập các lời giải của P1, …, PM
• Một lời giải thoả mãn ràng buộc
• Failure (tồn tại biến của miền giá trị rỗng)
Hình 2.6 Liệt kê các giá trị cho biến quyết định được lựa chọn đầu tiên
Hình 2.7 Cắt nhánh các miền
Hình 2.8 Tìm kiếm quay lui và cho kết quả Sơ đồ tổng quan của các bước tìm kiếm iii Một số chiến lược tìm kiếm
• Dom heuristic: chọn biến có miền giá trị nhỏ nhất
• Deg heuristic: chọn biến tham gia vào nhiều ràng buộc nhất
• Dom + deg heuristic: Áp dụng dom trước, sau đó áp dụng deg khi có nhiều biến có cùng kích thước miền giá trị nhỏ nhất
• Dom/deg: chọn biến có tỉ số dom/deg nhỏ nhất (kích thước miền giá trị/số ràng buộc mà biến tham gia vào)
Chiến lược chọn giá trị:
• Chọn giá trị theo thứ tựtăng dần
• Chọn giá trị theo thứ tự giảm dần
• Chọn giá trị ở giữa miền giá trị nhất iv Một số bài toán ví dụ CSP
Ví dụ 1: Bài toán con hậu N-Queens
Cho bàn cờkích thước n*n có n con hậu Cách sắp xếp n con hậu trên bàn cờ sao cho không có con nào có thểăn lẫn nhau
• Variables: X = {Xi | i ∈ [1, n]} một biến là đại diện cho một cột và ràng buộc mỗi con hậu phải trên một cột khác nhau
• Domains: Cho tất cả các biến Xi ∈ X, D(xi) = {1, 2, …, n}
• Constraints: Tập hợp các ràng buộc
2 con hậu không được cùng nằm trên một hàng
Hai con hậu không được cùng nằm trên một đường chéo
Ví dụ 2: Giải hệphương trình, bất phương trình
E Thư viện OR-Tools hỗ trợ giải TTP
OR-Tools là phần mềm mã nguồn mở chuyên dụng cho tối ưu tổ hợp, giúp tìm kiếm lời giải tốt nhất trong không gian giải pháp phong phú Phần mềm này có khả năng giải quyết nhiều bài toán khác nhau, mang lại hiệu quả cao trong việc tối ưu hóa.
• Vehicle routing: Tìm kiếm tối ưu đường đi cho phương tiện thoả mãn các ràng buộc
Lập lịch là quá trình tìm kiếm phương án tối ưu để sắp xếp các công việc phức tạp, trong đó một số nhiệm vụ cần được thực hiện trước trên các máy cố định hoặc tài nguyên khác.
CÁC PHƯƠNG PHÁP GIẢ I BÀI TOÁN L Ậ P L Ị CH THI ĐẤ U TH Ể THAO
Phương pháp Quy hoạ ch ràng bu ộ c
Trong luận văn này, chúng tôi áp dụng phương pháp quy hoạch ràng buộc và sử dụng công cụ OR-Tools để giải quyết bài toán TTP Mặc dù bài toán TTP có nhiều biến thể, chúng tôi tập trung vào bài toán cơ sở với các ràng buộc gốc, nhằm giảm thiểu số ràng buộc chặt, bao gồm việc “2 đội không được thi đấu với nhau trong 2 tuần liên tiếp và không được thi đấu trên sân nhà (sân khách) quá 3 tuần liên tiếp” Điều này giúp giảm độ phức tạp của bài toán Bài toán TTP sẽ được mô hình hóa trong chương trình Mixed-Integer Programming.
3.1.1 Mô hình hóa bài toán TTP
• duv là khoảng cách di chuyển từ sân của đội u đến sân của đội v
• 𝒊𝒊,𝒋𝒋,𝒖𝒖,𝒗𝒗 ∈ [𝟎𝟎…𝑻𝑻 − 𝟏𝟏]: là chỉ số của các đội
• 𝒕𝒕 ∈[𝟎𝟎…𝑾𝑾+𝟏𝟏]: Trong đó tuần 0 là tuần trước tuần thi đấu đầu tiên, tuần W+1 là tuần sau tuần thi đấu cuối cùng
• 𝑿𝑿𝒊𝒊𝒋𝒋𝒕𝒕∈{𝟎𝟎,𝟏𝟏}: Đội j có ở trên sân của đội I vào tuần thứ t hay không
- 𝑿𝑿 𝒊𝒊𝒊𝒊𝒕𝒕 =𝟏𝟏 nếu đội i ở trên sân nhà vào tuần t
- 𝑿𝑿𝒊𝒊𝒊𝒊𝟎𝟎 =𝑿𝑿𝒊𝒊𝒊𝒊 ( 𝑾𝑾+𝟏𝟏 )=𝟏𝟏 để đảm bảo đội i xuất phát tại sân nhà trước tuần đầu thi đấu đầu tiên và trở về sân nhà sau tuần cuối cùng
• 𝑭𝑭𝒊𝒊𝒖𝒖𝒗𝒗𝒕𝒕 ∈ { 𝟎𝟎,𝟏𝟏 } : Đội i di chuyển từ sân của đội u sang sân của đội v sau tuần thứ t hay không
• Mỗi đội i thi đấu đúng 1 trận mỗi tuần (cụ thể: hoặc là đội i ở trân sân của đội j ≠ i hoặc đội j ≠ i ở trên sân của đội i vào tuần thứ t):
• Đội i thi đấu trên sân nhà (tức là đội i ở trân sân của u = i) vào tuần t khi có một đội j thi đấu trân sân của i vào tuần đó:
Mỗi đội bóng j sẽ có một lần làm khách trên sân của đội i trong suốt mùa giải, tức là đội j sẽ thi đấu trên sân của đội i đúng một lần và ngược lại, đội i cũng sẽ tiếp đón đội j một lần duy nhất.
• Đội i di chuyển từ sân của u sang sân của v sau tuần t nếu i ở trên sân của u vào tuần t và ở trên sân của v vào tuần t+1
Để giảm thiểu hàm mục tiêu, cần tối ưu hóa thành phần Fiuvt, vì vậy bộ giải sẽ luôn chọn giá trị Fiuvt nhỏ nhất thỏa mãn điều kiện (5) Nếu điều kiện Xiut + Xiv(t+1) = 2 được thỏa mãn, tức là đội i thi đấu trên sân của u vào tuần t và trên sân của v vào tuần t+1, thì giá trị Fiuvt nhỏ nhất thỏa mãn (5) là 1 Ngược lại, ta có thể chọn Fiuvt = 0 mà vẫn đáp ứng điều kiện (5).
3.1.2 Cài đặt chương trình giải bài toán TTP sử dụng OR-Tools
Chương trình được cài đặt bằng ngôn ngữ Python
Bước 1: Đọc dữ liệu đầu vào
Dữ liệu đầu vào là một ma trận khoảng cách được đọc từ file with open('./SLSP/Schedule_Sport_N_4.txt') as f:
N = [int(x) for x in next(f).split()][0] print(N) d = [] for i in range(N): d.append([int(x) for x in next(f).split()]) print(d) f.close()
Bước 2: Khởi tạo bộ giải MIP và các biến quyết định
When selecting a MIP solver, choose variable x as the decision variable for the problem's constraints The variable f serves as a supplementary decision variable to x The solver can be initialized using the command: `solver = pywraplp.Solver('simple_mip_program', pywraplp.Solver.SCIP_MIXED_INTEGER_PROGRAMMING)`.
#Biến quyết định: Đội j có mặt trên sân i trong tuần t x = [[[solver.IntVar(0,1, 'x[%i][%i][%i]'%(i, j, t)) for t in range(2*N)]for j
Bướ c 3: Xây dựn g các ràng buộc cho bộ giải
#Contraints for i in range(N): solver.Add(x[i][i][0] == 1) solver.Add(x[i][i][2*N-1] == 1) solver.Add(sum(x[i][i][t] for t in range(1,2*N-1, 1)) == N-1) for j in range(N): if i != j: solver.Add(x[i][j][0] == 0) solver.Add(x[i][j][2*N - 1] == 0)
#Đội j làm khách đội i đúng 1 lần cả mùa giải solver.Add(sum(x[i][j][t] for t in range(2*N-1)) == 1) for v in range(N): for t in range(2*N -1):
#Đội i di chuyển từ sân u sang sân v sau tuần t solver.Add(f[i][j][v][t] >= x[j][i][t] + x[v][i][t+1] - 1) for t in range(2*N-1):
OnlyOneInWeek = solver.IntVar(0, solver.infinity(),
'OnlyOneInWeek[%i][%i]'%(i,t)) RivalInWeek = solver.IntVar(0, solver.infinity(),
'RivalInWeek[%i][%i]'%(i, t)) for j in range(N): if j != i:
#Đội j làm khách đội i đúng 1 lần cả mùa giải
#Mỗi đội i chỉthi đấu 1 trận một tuần solver.Add(OnlyOneInWeek == 1)
#Đội i thi đấu trên sân nhà solver.Add(x[i][i][t] == RivalInWeek)
Bước 4: Xây dựng hàm mục tiêu cho bộ giải in range(N)] for i in range(N)]
#Biến xác định di chuyển sau tuần t f = [[[[solver.IntVar(0,1, 'f[%i][%i][%i][%i]'%(i, u, v, t)) for t in range(2*N-1)]for v in range(N)]for u in range(N)]for i in range(N)]
Hàm mục tiêu được thiết lập dựa trên các biến quyết định kết hợp với dữ liệu đầu vào, nhằm tính toán tổng quãng đường di chuyển của tất cả các đội trong giải đấu Cụ thể, hàm này sẽ tối thiểu hóa tổng quãng đường di chuyển, được biểu diễn qua công thức: solver.Minimize(sum(f[i][u][v][t]*d[u][v] for i in range(N) for u in range(N) for v in range(N) for t in range(2*N-1))).
Bước 5: Thực thi bộ giải và biểu diễn kết quả status = solver.Solve() print('status:' ,status, pywraplp.Solver.OPTIMAL, pywraplp.Solver.INFEASIBLE) if status == pywraplp.Solver.OPTIMAL:
The objective value is displayed using the command `print('Objective value =', solver.Objective().Value())` A loop iterates through a range from 1 to 2*N-1, printing the week number with `print('tuan: ', t)` Within nested loops for indices i and j, the code checks if the solution value of `x[j][i][t]` equals 1, printing the corresponding indices if true If no optimal solution is found, it outputs 'problem does not have an optimal solution' Finally, the execution time is reported with the statement `print(" - %s seconds -" % (time.time() - start_time))`.
Phương pháp tìm kiế m c ụ c b ộ v ớ i thu ậ t toán SA
3.2.1 Ý tưởng của phương pháp SA trong bài toán TTP Đầu tiên chúng ta sẽ tìm cách tìm kiếm một giải pháp ban đầu thỏa mãn ràng buộc cho bài toán với thuật toán Đệ quy quay lui Sau đó sử dụng các phép biến đổi sẽđược đề cập ở phần sau, đi tìm các giải pháp lân cận và đánh giá vi phạm ràng buộc, chi phí di chuyển Qua đó, ghi nhận các giải pháp tiếp theo Vùng lân cận lớn có kích thước O(n 3 ), trong đó n là sốđội
Những phép biến đổi có thể tác động mạnh mẽ đến các phần khác trong giải pháp hiện tại Chẳng hạn, việc hoán đổi lịch trình của hai đội sẽ ảnh hưởng đến 4(n-2) giá trị trong cấu hình hiện tại Hơn nữa, một số biến đổi có thể tạo ra chuỗi phóng (ejection chains), thường được áp dụng trong tìm kiếm TABU.
SA sử dụng bộhâm nóng (reheat) để thoát khỏi cực tiểu cục bộở nhiệt độ thấp
Việc “hâm nóng’ lại làm tăng nhiệt độ và chia tìm kiếm thành nhiều giai đoạn
Việc áp dụng thuật toán SA để giải bài toán TTP được chúng tôi tham khảo từ
25 bài báo mục tiêu[13], với mô hình và các phép biến đổi chi tiết trong thuật toán được mô tảở phần 3.2.2
3.2.2 Mô hình bài toán TTP trong phương pháp SA
Bài toán TTP với kích thước n đội, sẽđược thi đấu vòng tròn trong (n-1)*2 tuần Trong đó:
Lịch thi đấu của đội t trong tuần w được biểu diễn với x > 0, cho thấy đội t thi đấu trên sân nhà, trong khi giá trị |x| đại diện cho đội đối thủ của đội t trong tuần đó.
Hình 3.1 Một lời giải cho bài toán TTP với kích thước n = 6
Qua đó ta có thể biểu diễn quãng đường di chuyển của từng đội như ví dụ dưới đây:
S1là quãng đường di chuyển trong suốt giải đấu của đội 1
Chi phí di chuyển được tính bằng tổng quãng đường C(S) = S1 + S2 + … + Sn Thuật toán sử dụng các phép biến đổi để tìm kiếm các giải pháp lân cận, từ đó phát hiện các phương án khả thi với chi phí giảm dần trong quá trình tối ưu hóa.
3.2.3 Các phép biến đổi tìm kiếm giải pháp lân cận
Trong thuật toán này, tác giả áp dụng năm phép biến đổi từ giải pháp hiện tại để tìm kiếm giải pháp láng giềng, trong đó SWAP_ROUNDS và SWAP_TEAM được xem là các phép biến đổi toàn phần, hoán đổi hầu hết các lịch trình giữa hai tuần hoặc hai đội trong mùa giải Sau khi thực hiện hoán đổi, giải pháp hiện tại cần tìm kiếm các thành phần bị ảnh hưởng và thực hiện biến đổi để đảm bảo lịch thi đấu vòng tròn hợp lệ Các phép biến đổi này có không gian tìm kiếm O(n²) Tuy nhiên, nhận thấy rằng SWAP_HOME, SWAP_ROUNDS và SWAP_TEAM chưa khai thác hết không gian tìm kiếm, tác giả đã đưa ra các phép biến đổi một phần như PATIAL_SWAP_ROUNDS và PATIAL_SWAP_TEAMS, với không gian hoán đổi O(n³) đủ để khám phá toàn bộ không gian tìm kiếm của bài toán TTP.
Phép biến đổi này thay đổi vai trò sân nhà và sân khách giữa hai đội Ti và Tj trong các tuần mà họ thi đấu với nhau Cụ thể, nếu đội Ti thi đấu trên sân nhà, điều này sẽ ảnh hưởng đến kết quả trận đấu.
Tj vào tuần Rk và chơi trên rân Tj và tuần Rl thì qua phép biến đổi này, lịch trình
26 trên sẽđảo ngược Ngoài ra các lịch thi đấu khác vẫn được giữnguyên Như vậy có tổng cộng O(n 2 ) phép biến đổi như vậy
Hình 3.2 Trước khi biến đổi SwapHomes(S, T 2 , T 4 )
Hình 3.3 Sau khi biến đổi SwapHomes(S, T 2 , T 4 )
Phép biến đổi này đơn giản là thay đổi lịch trình của tuần Rk và tuần Rl cho nhau Không gian của phép biến đổi này là O(n2)
Hình 3.4 Trước khi biến đổi SwapRounds(S, R 3, R 5 )
Hình 3.5 Sau khi biến đổi SwapRounds(S, R 3, R 5 )
Phép biến đổi này sẽ hoán đổi lịch thi đấu giữa hai đội Ti và Tj, ngoại trừ các tuần mà hai đội này đối đầu nhau Sau khi thực hiện hoán đổi, lịch thi đấu của các đội khác sẽ được điều chỉnh để đảm bảo tính hợp lệ của giải pháp.
Với 3 bước di chuyển trên, không đủđể khám phá toàn bộ không gian tìm kiếm, do đó về lý thuyết chúng không đủ tìm thấy giải pháp tối ưu cho bài toán TTP Vì thế, cần phải có các phép biến đổi tổng quát hơn Đó là những phép biến đổi từng phần với sự biến đổi chi tiết và tinh vi hơn.
Hình 3.6 Trước khi biến đổi SwapTeams(S, T 2 , T 4 )
Hình 3.7 Sau khi biến đổi SwapTeams(S, T 2 , T 4 )
Phép biến đổi này thay đổi lịch thi đấu của đội Ti giữa hai tuần Rk và Rl, sau đó cập nhật lại các lịch bị ảnh hưởng trong giải pháp hiện tại Việc xác định các lịch bị ảnh hưởng có thể dẫn đến một chuỗi phóng, với không gian của phép biến đổi này là O(n^3).
Hình 3.8 Trước khi biến đổi PartialSwapRounds(S, T 2 , R 2, R 9 )
Hình 3.9 Sau khi biến đổi PartialSwapRounds(S, T 2 , R 2 , R 9 )
Phép biến đổi này thực hiện việc hoán đổi lịch thi đấu giữa đội Ti và Tj trong tuần Rk Sau đó, quá trình tìm kiếm các thành phần bị ảnh hưởng và cập nhật lại được tiến hành để tạo ra một giải pháp mới đáp ứng các ràng buộc Phép biến đổi này có độ phức tạp không gian O(n^3).
Hình 3.10 Trước khi biến đổi PartialSwapTeams(S, T 2 , T 4 , R 9 )
Hình 3.11 Sau khi biến đổi PartialSwapTeams(S, T 2 , T 4 , R 9 )
3.2.4 Biểu đồ hoạt động thuật toán SA giải TTP
Thuật toán Simulated Annealing (SA) là một kỹ thuật meta-heuristic dùng để khám phá các vùng lân cận Quy trình bắt đầu từ một giải pháp ngẫu nhiên, được tạo ra thông qua một tìm kiếm Back-Tracking đơn giản, cho phép dễ dàng thu được một lịch trình khả thi Bước khởi đầu này là rất quan trọng trong hoạt động của thuật toán.
Hình 3.12 Thuật toán đệ quy khởi tạo giải pháp ban đầu ngẫu nhiên
Hình 3.13 Biểu đồ hoạt động thuật toán khởi tạo giải pháp khả thi ban đầu cho bài toán
• Q: Danh sách lịch thi đấu của các đội t trong tuần w chưa được khởi tạo giá trị
• S: Biến biểu diễn giải pháp tìm thấy
• Choices: Tập giá trị được phép chọn để xem sét khởi tạo giá trị cho đội t trong tuần w
Áp dụng lược đồ bài toán luyện thép truyền thống, thuật toán sẽ chọn ngẫu nhiên một phép biến đổi tại nhiệt độ T để tìm ra giải pháp lân cận Sự biến thiên Δ trong hàm mục tiêu được tạo ra từ phép biến đổi này, và nếu Δ nhỏ hơn một ngưỡng nhất định, quá trình sẽ tiếp tục được thực hiện.
0, phải pháp lân cận được chấp nhận và quá trình luyện thép tiếp tục Nếu không, giải pháp lân cận sẽđược cân nhắc chấp nhận với xác suất exp(-Δ/T).
Trong thuật toán luyện thép, xác suất chấp nhận giải pháp không cải thiện giảm dần theo thời gian Hiện tượng này đạt được bằng cách giảm nhiệt độ Thuật toán sử dụng bộ đếm có thể thay đổi, tăng dần cho mỗi lần biến đổi không cải thiện, và được đặt lại về 0 khi giải pháp tốt nhất được cải thiện Khi bộ đếm đạt giới hạn cụ thể, nhiệt độ được cập nhật thành T*β, với β là hằng số cố định nhỏ hơn 1.
Bộđếm lại được đặt về 0
Cấu trúc thuật toán SA điển hình được mô tảnhư sau:
Hình 3.14 Thuật toán SA điển hình
Kết hợp thuật toán SA và thuật toán khởi tạo gia trị ban đầu cho bài toán TTP, ta có mô hình cài đặt như sau:
Hình 3.15 Thuật toán SA áp dụng cho TTP
Hình 3.16 Biểu đồ hoạt động của thuật toán SA cho bài toán TTP
• Hàm đánh giá chi phí của giải pháp được mô tảnhư trong công thức sau: 𝐶𝐶(𝑆𝑆) � 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐(𝑆𝑆)𝑛𝑛ế𝑢𝑢 𝑆𝑆 𝑐𝑐ℎỏ𝑚𝑚 𝑚𝑚ã𝑛𝑛 𝑟𝑟ã𝑛𝑛𝑛𝑛 𝑟𝑟à𝑛𝑛𝑛𝑛 𝑏𝑏𝑢𝑢ộ𝑐𝑐
• nbv(S) là hàm tính số lần vi phạm
• 𝜔𝜔 là trọng số sẽđược thay đổi trong suốt quá trình luyện thép
• f: N → N là 1 hàm con tuyến tính sao cho f(1) = 1, f(v) = 1+ √𝑛𝑛ln(v/2) Hàm f có mục tiêu giúp chương trình không cập nhật quá chậm để tránh những giải pháp không khả thi
• nbf: Giá trị chi phí khả thi tốt nhất được ghi nhận
• nbi: Giá trị chi phí không khả thi tốt nhất được ghi nhận
• T: nhiệt độ T trong thuật toán SA
• β: Hằng số biến đổi T trong quá trình luyện thép
• θ: Hằng số biến đổi 𝜔𝜔trong trường hợp tìm thấy giải pháp khả thi tốt hơn
• δ: Hằng số biến đổi 𝜔𝜔 trong trường hợp tìm thấy giải pháp không khả thi tốt hơn
KẾ T QU Ả TH Ự C NGHI Ệ M
Các tiêu chí th ự c nghi ệ m
Mục tiêu của chúng tôi trong nghiên cứu này là xác định khả năng của phương pháp quy hoạch ràng buộc, hỗ trợ bởi công cụ Or-Tools, trong việc giải quyết hiệu quả bài toán TTP Bên cạnh đó, chúng tôi cũng nghiên cứu áp dụng thuật toán SA để tìm ra giải pháp gần đúng và kiểm chứng kết quả theo bài báo mục tiêu [13] Qua đó, chúng tôi đánh giá hiệu quả của các phương pháp giải bài toán TTP, từ đó mở ra hướng đi cho việc kết hợp với các phương pháp khác trong tương lai.
Bài toán TTP là một thách thức lớn với nhiều ràng buộc, tạo ra một không gian tìm kiếm rộng rãi ngay cả khi kích thước bài toán nhỏ Trong khuôn khổ luận văn của chúng tôi, chúng tôi chỉ giới hạn nghiên cứu ở các kích thước từ 4 đến 16, với n là số chẵn.
Chúng tôi thực hiện kiểm thử cho từng mẫu theo các phương pháp khác nhau bằng cách chạy giải toán 30 lần và ghi nhận kết quả tốt nhất Mỗi lần thử nghiệm được giới hạn trong thời gian 48 giờ.
Các mẫu dữ liệu từ 4.1 đến 4.10 được tạo ra nhằm làm phong phú thêm tập kiểm thử khi áp dụng Or-Tools cho bài toán TTP Trong khi đó, các mẫu dữ liệu NL4 đến NL16 được thu thập từ challenge [3], phục vụ như những tài nguyên chung cho các nhà nghiên cứu trên toàn cầu trong lĩnh vực này.
Cả 2 phương pháp được áp dụng giải bài toán TTP đều được lập trình trên ngôn ngữ Python Máy thực hiện có thông số Chip I7-6700HQ, Ram 16GB
Hình 4.1 Thông số thiết bị thực nghiệm
k ế t qu ả khi áp d ụ ng Or-Tools gi ả i bài toán TTP
Giải TTP tối giản ràng buộc được thực hiện bằng cách loại bỏ các quy định nghiêm ngặt như: "Hai đội không được thi đấu liên tiếp trong 2 tuần và không được thi đấu trên sân nhà hoặc sân khách quá 3 tuần liên tiếp." Dữ liệu được tạo ra với số lượng đội từ 4 đến 10 đội, và thời gian giới hạn cho việc thực hiện là 48 giờ.
Bảng 4.1 Kết quả và thời gian thực nghiệm khi sử dụng Or-Tools
Time run of OR- tools(s)
Giải thích số liệu trong bảng 4.1:
• Data: các mẫu dữ liệu thử nghiệm khi sử dụng Or-Tools
• Cost of Unconstrained Feasible Solution: kết quả tốt ưu khi áp dụng Or-Tools giải bài toán TTP không có ràng buộc chặt
• Time run of OR-tools(s): Thời gian chạy chương trình
Or-Tools thể hiện hiệu quả tối ưu với các bộ dữ liệu nhỏ, cho kết quả trong thời gian ngắn Tuy nhiên, khi kích thước bài toán tăng lên, không gian tìm kiếm mở rộng khiến chương trình không thể hoàn thành trong thời gian giới hạn Do đó, chúng tôi đã quyết định không sử dụng Or-Tools cho các mẫu thử lớn hơn.
Công cụ Or-Tools hiện vẫn còn hạn chế khi áp dụng vào bài toán tối ưu tổ hợp phức tạp với nhiều ràng buộc, như bài toán TTP Việc tìm ra kết quả tối ưu trong thời điểm hiện tại là điều không khả thi Do đó, trong bài luận này, chúng tôi sẽ chuyển sang sử dụng các kỹ thuật metaheuristic để tìm kiếm kết quả tốt nhất có thể trong khoảng thời gian cho phép, đặc biệt là đối với các bài toán có kích thước lớn hơn (n>4).
K ế t qu ả khi áp d ụ ng gi ả i thu ậ t SA gi ả i bài toán TTP
Sử dụng Simulated Annealing (SA) để giải bài toán TTP với kích thước n=4 là nhanh chóng và dễ dàng, giúp tìm ra phương án tối ưu Tuy nhiên, với kích thước này, độ phức tạp không cao, dẫn đến việc các mẫu thử n=4 không thể hiện sự khác biệt rõ rệt giữa hai phương pháp Vì vậy, trong thực nghiệm SA, chúng tôi đã áp dụng các mẫu dữ liệu có kích thước lớn hơn, từ NL4 đến NL16.
Việc sử dụng SA giải bài toán TTP luôn cho kết quả khả khi với kích thước bài toán n 12 (NL14, NL16), quá trình thực nghiệm chưa tìm được lời giải thỏa mãn trong 48 giờđối với bài toán TTP có ràng buộc chặt
Hình 4.2 Biểu đồ thống kê tốc độ hội tụ hàm mục tiêu với dữ liệu NL12
Kết quả từ 30 lần chạy thử với dữ liệu NL12 cho thấy tốc độ hội tụ của hàm mục tiêu trong khoảng thời gian từ 0 đến 10.000 giây khá nhanh Tuy nhiên, sau thời gian này, khả năng tìm kiếm giải pháp tốt hơn bắt đầu chậm lại.
Hình 4.3 So sánh tốc độ hội tụ của bài toán TTP có ràng buộc chặt và không có
Trong nghiên cứu này, chúng tôi đã thực hiện phép so sánh dựa trên 10 lần chạy thử dữ liệu NL12 Kết quả cho thấy, đường đỏ biểu thị thống kê của giải pháp có ràng buộc chặt, trong khi đường xanh đại diện cho giải pháp không có ràng buộc chặt.
Theo biểu đồ Hình 4.3, trong bài toán không có ràng buộc chặt, thuật toán SA cho kết quả tìm kiếm ban đầu nhanh hơn và chi phí thấp hơn Tuy nhiên, sau đó, tốc độ tìm kiếm của hai trường hợp trở nên khá tương đồng Bài toán không có ràng buộc chặt vẫn mang lại kết quả tốt hơn một chút về chi phí.
Bảng 4.3 Các tham số được chọn khi sử dụng SA cho bài toán TTP
Data T0 β Wo δ θ maxC maxP maxR γ
NL10 400 0.9999 6000 1.04 1.04 5000 7100 3 2 NL12 700 0.9999 60000 1.05 1.05 5000 7100 3 2 NL14 600 0.9999 20000 1.05 1.05 4000 7100 3 2 NL16 700 0.9999 60000 1.05 1.05 10000 7100 3 2 Các tham sốđược tham khảo [13]
So sánh kết quả thực nghiệm với kết quả của bài báo mục tiêu khi thực hiện giải bài toán TTP sử dụng thuật toán SA:
Bảng 4.4 So sánh kết quả thực nghiệm với kết quả của bài báo đề xuất
Data Tốt nhất của bài báo Kết quả thực nghiệm
Trong quá trình cài đặt giải thuật SA cho bài toán TTP, sự khác biệt về cấu trúc dữ liệu, ngôn ngữ lập trình và số lần training kiểm thử đã dẫn đến việc kết quả ghi nhận trong luận văn chưa đạt giá trị tối ưu như trong bài báo nguồn Dù vậy, thuật toán vẫn thể hiện đúng tính chất và cho thấy hiệu quả trong việc cải thiện kết quả tìm kiếm trong thời gian cho phép đối với bài toán TTP.
Chúng tôi đã thực hiện các thí nghiệm loại bỏ một số thành phần trong thuật toán để phân tích tác dụng của chúng và đo lường mức độ quan trọng của từng thành phần đối với hiệu suất chất lượng của thuật toán Phương pháp thực nghiệm này được tham khảo từ nghiên cứu trong bài báo mục tiêu [13].
Bảng 4.5 Tác động của các thành phần TTSA đến chất lượng giải pháp (12 đội)
Tốt nhất Tệ nhất Trung bình Độ lệch chuẩn
Trong nghiên cứu này, các phiên bản SA được phân loại như sau: SA là phiên bản đầy đủ với tất cả các thành phần, SA(PS) chỉ xem xét một phần biến đổi, SA(NR) không bao gồm thành phần hâm nóng, và SA(Các phiên bản T) giữ nguyên nhiệt độ trong suốt quá trình tìm kiếm Tất cả các phiên bản này đã được thực hiện trong 30 lần với giới hạn thời gian là 100000 giây, sử dụng mẫu NL12.
Theo bảng số liệu, phiên bản đầy đủ của thuật toán SA cho kết quả tốt nhất Việc thực hiện cả bước di chuyển đầy đủ lẫn một phần mang lại lợi ích lớn hơn so với chỉ xem xét bước di chuyển một phần, nhờ vào sự đa dạng hóa trong các chuyển động Quá trình hâm nóng cũng cho thấy hiệu quả, khi giảm giá trị trung bình từ 160000 xuống 150000 Các phiên bản giữ nguyên nhiệt độ cũng chứng minh tính hiệu quả của thuật toán SA, với việc cập nhật giảm nhiệt độ liên tục giúp cải thiện kết quả hội tụ.
Các tham sốđầu vào của phép thực nghiệm này được thể hiện trong bảng sau:
Bảng 4.6 Các tham số đầu vào phép thử tác động thành phần
Phiên bản T 0 β Wo δ θ maxC maxP maxR γ
SA 1100 999 18000 01.03 01.03 3000 710 1000 1.4 SA(PS) 1100 999 18000 01.03 01.03 3000 710 1000 1.4 SA(NR) 1100 9.999 18000 01.03 01.03 3000000 ∞ 0 1
KẾ T LU Ậ N
K ế t lu ậ n
Trong luận văn này, chúng tôi nghiên cứu bài toán Lập lịch thi đấu thể thao, bắt đầu bằng việc sử dụng các công cụ tối ưu như Or-Tools Kết quả thực nghiệm cho thấy, mặc dù đã giảm bớt độ phức tạp của các ràng buộc, phương pháp này chỉ cho phép giải tối ưu với kích thước n = 4 Khi n > 4, thời gian giải vượt quá 48 giờ, cho thấy sự bất khả thi trong việc tìm ra giải pháp tối ưu Qua nghiên cứu, chúng tôi nhận thấy việc giải bài toán TTP trở nên thách thức lớn khi kích thước tăng Do đó, chúng tôi quyết định áp dụng phương pháp giải gần đúng để tìm kiếm kết quả chấp nhận được và cải thiện giá trị hàm mục tiêu, với bước tiếp theo là nghiên cứu và cài đặt thuật toán tôi thép được đề xuất.
A Anagnostopoulos, L Michel, P Van Hentenryck và Y Vergados năm 2003 và tiến hành thực nghiệm đánh giá kết quả Kết quả thực nghiệm trong khuôn khổ luận văn mặc dù chưa tìm được các kết quả tốt như bài báo mô tả, tuy nhiên các đặc trưng của thuật toán cũng như tính khả thi khi tìm ra và cải thiện giá trị hàm mục tiêu đều thể hiện được cho thấy thuật toán SA có hiệu quả trong việc liên tục cải thiện các giải pháp lập lịch thi đấu, đưa ra được các phương án khả thi đối với kích thước bài toán n = 16 trở xuống SA cho khảnăng vượt trội hơn Or-Tools trong việc giải bài toán TTP.
Hướ ng phát tri ể n c ủa đồ án trong tương lai
Bài toán TTP đã thu hút sự chú ý của nhiều nhà khoa học trên toàn thế giới, với nhiều phương pháp và biến thể khác nhau được nghiên cứu Một ví dụ điển hình là việc cải tiến thuật toán Simulated Annealing (SA) để tăng tốc độ tìm kiếm, cũng như việc kết hợp SA với thuật toán tìm kiếm Tabu, như trong nghiên cứu “Solving the Traveling Tournament Problem Based on the Simulated Annealing and Tabu Search Algorithm” Chúng tôi cam kết tiếp tục nghiên cứu nhằm cải thiện kết quả thực nghiệm cho bài toán này trong tương lai.