NHẬN DẠNG HÀM TRUYỀN TRÊN TOOLBOX IDENTIFICATION SYSTEM THIẾT KẾ BỘ ĐIỀU KHIỂN PD MỜ THIẾT KẾ MẠNG THẦN KINH XẤP XỈ MỜ ÁP DỤNG GIẢI THUẬT DI TRUYỀN TÌM THÔNG SỐ BỘ PID,Điều khiển mạng thần kinh hay Neural là phương pháp điều khiển dựa theo cấu tạo của mạng thần kinh trong thực tế. Trong đó có nhiều lớp, mỗi lớp bao gồm nhiều nơron có cùng một chức năng
BỘ GIÁO DỤC & ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP HỒ CHÍ MINH KHOA ĐIỆN – ĐIỆN TỬ BỘ MÔN TỰ ĐỘNG ĐIỀU KHIỂN -⸙∆⸙ - NHẬN DẠNG VÀ ĐIỀU KHIỂN HỆ THỐNG ĐỀ TÀI: NHẬN DẠNG HÀM TRUYỀN TRÊN TOOLBOX IDENTIFICATION SYSTEM GVHD: TRẦN ĐỨC THIỆN SVTH: PHAN MINH ĐIỀN MSSV: 19151037 Tp Hồ Chí Minh tháng năm Lời cảm ơn Mục lục Lời cảm ơn i Mục lục ii Danh sách hình ảnh .iii Danh sách bảng iv Chương THIẾT KẾ BỘ ĐIỀU KHIỂN PD MỜ 1.1 MƠ TẢ TỐN HỌC HỆ CÁNH TAY MÁY BẬC 1.2 CƠ SỞ LÝ THUYẾT 1.3 XÂY DỰNG MÔ PHỎNG PD MỜ 1.4 KẾT QUẢ MÔ PHỎNG 12 Chương THIẾT KẾ MẠNG THẦN KINH XẤP XỈ MỜ 19 2.1 CƠ SỞ LÝ THUYẾT 19 2.2 XÂY DỰNG MÔ PHỎNG MẠNG THẦN KINH XẤP XỈ MỜ 21 2.3 KẾT QUẢ MÔ PHỎNG 23 Chương ÁP DỤNG GIẢI THUẬT DI TRUYỀN TÌM THƠNG SỐ BỘ PID 27 3.1 CƠ SỞ LÝ THUYẾT 27 3.2 XÂY DỰNG MÔ PHỎNG 28 TÀI LIỆU THAM KHẢO 35 Danh sách hình ảnh No table of figures entries found Danh sách bảng Bảng 1-1: Hệ quy tắc mờ cánh tay máy bậc CHƯƠNG THIẾT KẾ BỘ ĐIỀU KHIỂN PD MỜ Chương 1.THIẾT KẾ BỘ ĐIỀU KHIỂN PD MỜ 1.1 MƠ TẢ TỐN HỌC HỆ CÁNH TAY MÁY BẬC Ta xét robot trạng thái bỏ qua ma sát khớp, bỏ qua tác động lực vào khớp cuối robot Hình 1.1: Mơ tả hệ cánh tay máy bậc Thông số vật lý cánh tay máy mô phỏng: J1 , J : moment quán tính hai khớp J1 0.05kg m ; J 0.05kg m m1 , m2 : khối lượng hai khớp m1 1.0kg ; m2 1.0kg l1 , l2 : chiều dài hai khớp l1 1.0m; l2 1.0m lc1 , lc : khoảng cách từ trọng tâm khớp đến trục quay lc1 0.4m; lc 0.4m g : gia tốc trọng trường g 9.81m / s Ta đặt trục toạ độ đế cánh tay máy Như vị trí Vị trí cuối Link robot là: x1 l1 cos 1 y1 l1 sin 1 (1.1) Vị tri cuối Link robot là: x2 l1 cos 1 l2 cos(1 2 ) y2 l1 sin 1 l2 sin(1 2 ) (1.2) Trọng tâm Link so với đế robot là: ĐIỀU KHIỂN THÔNG MINH CHƯƠNG THIẾT KẾ BỘ ĐIỀU KHIỂN PD MỜ xc1 lc1 cos 1 (1.3) yc1 lc1 sin 1 Trọng tâm Link so với đế robot là: xc2 l1 cos 1 lc2 cos(1 2 ) (1.4) yc2 l1 sin 1 lc2 sin(1 2 ) Vận tốc điểm cuối Link x1 l11 sin 1 (1.5) y1 l11 cos 1 Vận tốc điểm cuối Link x2 l11 sin 1 l2 1 2 sin 1 2 (1.6) y2 l11 cos 1 l2 1 2 cos 1 2 Tốc độ góc ứng với Link1 Link 1 1 (1.7) 2 1 Động Link K1 1 1 m1v12 J112 m1 x12 y12 J112 2 2 (1.8) Thay (1.5) vào (1.8), ta được: K1 m1 lc 1 sin 1 l cos 1 J112 2 c1 (1.9) Biến đổi tương đương (1.9):, ta rút gọn phương trình động Link K1 m1 1lc1 J112 (1.10) Động Link là: K2 1 1 m2 v22 J 22 m2 x22 y22 J 1 2 2 2 (1.11) Thay (1.6), vào (1.11), ta được: m2 l11 sin 1 lc2 1 2 sin 1 2 2 l11 cos 1 lc2 1 2 cos 1 J 1 2 K1 (1.12) Từ (1.12), ta động Link K1 m2 1l1 lc2 ĐIỀU KHIỂN THÔNG MINH 21l1 1 2 lc2 cos 2 J 1 2 (1.13) CHƯƠNG THIẾT KẾ BỘ ĐIỀU KHIỂN PD MỜ Như ta tính tổng động hệ là: K K1 K m1 1lc1 m2 1l1 1 J 12 J 1 2 2 2 lc2 (1.14) 21l1 1 2 lc2 cos 2 Thế Link P1 m1 gyc m1 glc1 sin 1 (1.15) P2 m2 gyc m2 g lc sin 1 lc2 sin 1 2 (1.16) Thế Link 2: Tổng hệ là: P P1 P2 m1 glc1 sin 1 m2 g lc sin 1 lc2 sin 1 2 (1.17) Phương trình Lagrange ứng với robot hai bậc tự do: L , K P 2 1 m1 1lc1 I zz112 J 1 2 m1 glc1 s1 m2 g lc s1 lc2 s12 2 2 m2 1l1 1 2 lc2 21l1 1 2 lc2 c2 (1.18) Trong đó: K động robot, P hệ Tiến hành đặt:, si sin(i ) , c j cos( j ) , sij sin(i j ) Theo phương trình Lagrange ta thành lập phương trình phi tuyến Tổng Momen (torque) Link 1 d L L dt 1 1 (1.19) Giải phương trình ta 1 J1 J m1lc12 m2 l12 m2 lc 2 2m2 l1lc cos 2 1 J m2 lc 2 m2 l1lc cos 2 2 l1lc m2 sin 2 212 2 (1.20) m1 m2 glc1 cos 1 m2 glc cos 1 2 Tổng Momen (torque) Link 2 d L dt 2 L 2 (1.21) Giải phương trình ta được: ĐIỀU KHIỂN THÔNG MINH CHƯƠNG THIẾT KẾ BỘ ĐIỀU KHIỂN PD MỜ 2 J m2 lc 2 m2 l1lc cos 2 1 m2 lc 2 J 2 m2 l1lc 12 sin 2 m2 glc cos 1 2 (1.22) Phương trình động học gồm ma trận: M C , G (1.23) Với: M ma trận quán tính, C , vector hướng tâm/ Coriolis, G vector trọng lực J1 J m1lc12 m2 l12 lc 2 2l1lc c2 J m2 lc 2 l1lc c2 M 2 J m l l l c J m l 2 c2 c2 2 c2 l1lc m2 s 2 C , l1lc m2 s 1 l1lc m2 s 1 2 (1.24) (1.25) m m2 glc1 c1 m2 glc c12 G m2 glc c12 (1.26) , , 2 2 2 (1.27) Trong đó: si sin(i ) , c j cos( j ) , sij sin(i j ) , cij cos(i j ) Để dễ dàng lập trình ta đặt ma trận sau: H11 H 21 H12 1 h H 22 h1 h1 h 1 g1 g (1.28) Trong đó: H11 J1 J m1lc12 m2 l12 lc 2 2l1lc c2 (1.29) H 22 J m2 lc 2 (1.30) H12 H 21 J m2 lc 2 l1lc c2 (1.31) h m2 l2 lc s2 (1.32) g1 m1lc1 gc1 m2 g lc c 1 l1c1 (1.33) g m2 lc gc 1 (1.34) 1.2 CƠ SỞ LÝ THUYẾT Một hệ mờ biểu diễn theo hình bên dưới: ĐIỀU KHIỂN THƠNG MINH CHƯƠNG THIẾT KẾ MẠNG THẦN KINH XẤP XỈ MỜ 2.2 XÂY DỰNG MÔ PHỎNG MẠNG THẦN KINH XẤP XỈ MỜ Cấu trúc điều khiển: Hình 2.5: Sơ đồ khối Cấu trúc điều khiển mạng thàn kinh xấp xỉ mờ Sơ đồ mơ phỏng: Hình 2.6: Sơ đồ hệ thu thập liệu PD mờ Các khối To Workspace lấy liệu đưa vệ dạng ma trận : ĐIỀU KHIỂN THÔNG MINH 21 CHƯƠNG THIẾT KẾ MẠNG THẦN KINH XẤP XỈ MỜ Hình 2.7: Đặt tên biến , dạng biến cho tín hiệu Sau thu thập liệu ta tiến hành thực Code Matlab để tìm xấp xỉ PID mờ % code neuron_nhóm 18 ngovao = vaolink1'; % khai báo ngõ vào ngora = ralink1'; % khai báo ngõ net = newff(minmax(ngovao),[40 1],{'tansig' 'purelin'}); % khởi tạo mạng truyền thẳng lớp % lớp ẩn , lớp đại diện cho ngõ , hàm kích hoạt lớp ẩn % tansig, hàm kích hoạt lớp hàm purelin (hàm tuyến %tính) net.trainParam.epochs = 10000;% số lần train net.trainParam.lr = 0.000000001;% hệ số học net.trainParam.goal = 0.000001;% sai số net = train(net,ngovao,ngora);%khởi tạo mạng thần kinh gensim(net,0.01) % training mạng thần kinh với thời gian lấy mẫu 0.01 ĐIỀU KHIỂN THÔNG MINH 22 CHƯƠNG THIẾT KẾ MẠNG THẦN KINH XẤP XỈ MỜ Từ khối neuron từ chương trình trên, gắn vào điều khiển: Hình 2.8: Sơ đồ Simulink điều khiển Neural 2.3 KẾT QUẢ MÔ PHỎNG Sau thay PD mờ điều khiểun Neural xấp xỉ, ta thu đồ thị sau: - Đáp ứng ngõ Hình 2.9: Đáp ứng ngõ link thứ ĐIỀU KHIỂN THÔNG MINH 23 CHƯƠNG THIẾT KẾ MẠNG THẦN KINH XẤP XỈ MỜ Hình 2.10: Đáp ứng ngõ link thứ - Tín hiệu điều khiển: Hình 2.11: Tín hiệu điều khiển u link ĐIỀU KHIỂN THÔNG MINH 24 CHƯƠNG THIẾT KẾ MẠNG THẦN KINH XẤP XỈ MỜ Hình 2.12: Tín hiệu điều khiển u link Sai số hệ thống: Hình 2.13: Sai số e link ĐIỀU KHIỂN THÔNG MINH 25 CHƯƠNG THIẾT KẾ MẠNG THẦN KINH XẤP XỈ MỜ Hình 2.14: Sai số e link Nhận xét: Với điều khiển mạng thần kinh xấp xỉ PD mờ ta có đáp ứng hệ thống: - Cánh tay thứ bám tín hiệu ổn sai số cịn cao khơng đáng kể - Cánh tay bám tín hiệu tốt , bị nhiễu vị trí độ - Thời gian đáp ứng cánh tay nằm khoảng 5s Như điều khiển thần kinh xấp xỉ PD áp dụng để điều khiển cho hệ cánh tay máy bậc ĐIỀU KHIỂN THÔNG MINH 26 CHƯƠNG ÁP DỤNG GIẢI THUẬT DI TRUYỀN TÌM THÔNG SỐ BỘ PID Chương 3.ÁP DỤNG GIẢI THUẬT DI TRUYỀN TÌM THƠNG SỐ BỘ PID 3.1 CƠ SỞ LÝ THUYẾT Giải thuật di truyền GA giải thuật tìm kiếm lời giải tối ưu theo trình tiến hóa sinh vật tự nhiên Hình 3.1: Bài tốn dùng giải thuật GA Bài tốn tối ưu hóa cần giải lĩnh vực điều khiển: J (3.1) Với 1 , , , n T Hàm thích nghi J , phần báo cáo có dạng: fitness f x1 , x2 C (3.2) Mã hoá theo dạng thập phân với qui ước: - Giá trị gene =0→4 mang dấu trừ (-) - Giá trị gene =5→9 mang dấu cộng (-) - Mỗi lời giải tốn tìm cực trị cặp x1 , x2 mã hóa thành chuỗi NST có dạng sau: ĐIỀU KHIỂN THÔNG MINH 27 CHƯƠNG ÁP DỤNG GIẢI THUẬT DI TRUYỀN TÌM THƠNG SỐ BỘ PID Hình 3.2: Chuỗi mã hoá thập phân Khởi động: Thế hệ ngẫu nhiên Các thông số giải thuật di truyền: - Kích thước quần thể: N 20 - Chọn lọc hạng tuyến tính: pk - N k 1 1 N (3.3) Cường độ chọn lọc I 1 - Xác suất lai ghép: Lai ghép điểm với xác suất pc 0.9 - Xác suất đột biến: Đột biến dạng phân với xác suất pm 0.1 - Lưu giữ NST ưu việt trình tiến hóa (3.4) Số lượng NST 3.2 XÂY DỰNG MƠ PHỎNG Hình 3.3: Mơ hình hố hệ cánh tay máy bậc ĐIỀU KHIỂN THÔNG MINH 28 CHƯƠNG ÁP DỤNG GIẢI THUẬT DI TRUYỀN TÌM THƠNG SỐ BỘ PID Hình 3.4: Xây dựng mơ giải thuật GA tìm thơng số PID Code GA tìm PID: clc; clear all rand('state',sum(100*clock)); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%thong so m1=1; m2=1; m3=0; l1=1; l2=1; lc1=0.4; lc2=0.4; g=9.81; the1_dnit=0; the2_dnit=0; the1_nit=0; the2_nit=0; %%%%%%%%%%%%%%%%%%%%%%%%%%%% max_generation=2000; %% có 2000 lan chay q trình max_stall_generation=50; %% 50 the he giong dung epsilon=0.0001; %% J chuan ( neu the he có J1, ĐIỀU KHIỂN THÔNG MINH 31 CHƯƠNG ÁP DỤNG GIẢI THUẬT DI TRUYỀN TÌM THÔNG SỐ BỘ PID if abs(bestfit(generation)-bestfit(generation1))NHẬN DẠNG HÀM TRUYỀN TRÊN TOOLBOX IDENTIFICATION SYSTEM
41
6
0
THÔNG TIN TÀI LIỆU
Thông tin cơ bản
| Tiêu đề | Nhận Dạng Hàm Truyền Trên Toolbox Identification System |
|---|---|
| Tác giả | Phan Minh Điền |
| Người hướng dẫn | GVHD: Trần Đức Thiện |
| Trường học | Trường Đại Học Sư Phạm Kỹ Thuật Tp. Hồ Chí Minh |
| Chuyên ngành | Điện – Điện Tử |
| Thể loại | đề tài |
| Thành phố | Tp. Hồ Chí Minh |
| Định dạng | |
|---|---|
| Số trang | 41 |
| Dung lượng | 2,76 MB |
Nội dung
Ngày đăng: 22/10/2022, 16:47
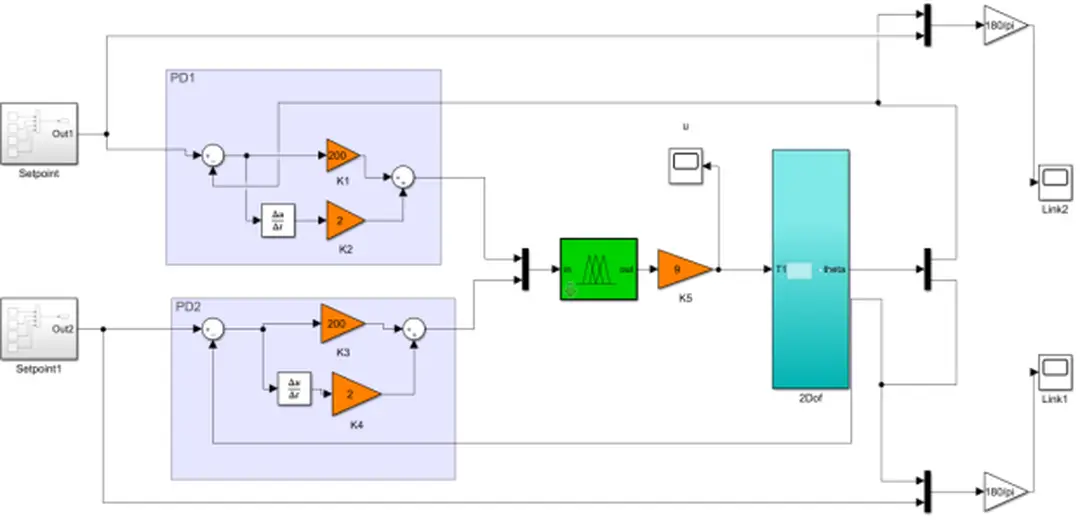
HÌNH ẢNH LIÊN QUAN














TÀI LIỆU CÙNG NGƯỜI DÙNG
-
58 2 0
-
5 8 0
-
5 13 0
-
52 5 0
TÀI LIỆU LIÊN QUAN
-
41 6 0
-
13 9 0
-
78 12 0
-
1 10 0
-
2 28 0
-
1 40 1
-
1 16 0
-
2 34 0