Một số phương pháp tiếp cận cho bài toán lập lịch cá nhân
31
7
0
THÔNG TIN TÀI LIỆU
Thông tin cơ bản
| Tiêu đề | Một Số Phương Pháp Tiếp Cận Cho Bài Toán Lập Lịch Cá Nhân |
|---|---|
| Tác giả | T. H. Son, T. V. Lang, N. Huynh-Tuong |
| Người hướng dẫn | PGS. TS. Trần Văn Lăng, PGS. TS. Huỳnh Tường Nguyên |
| Trường học | Đại học Quốc gia TP. Hồ Chí Minh Trường Đại học Bách Khoa |
| Chuyên ngành | Khoa học máy tính |
| Thể loại | Luận án tiến sĩ |
| Năm xuất bản | 2022 |
| Thành phố | TP. Hồ Chí Minh |
| Định dạng | |
|---|---|
| Số trang | 31 |
| Dung lượng | 503,51 KB |
Nội dung
Ngày đăng: 19/10/2022, 23:57
HÌNH ẢNH LIÊN QUAN












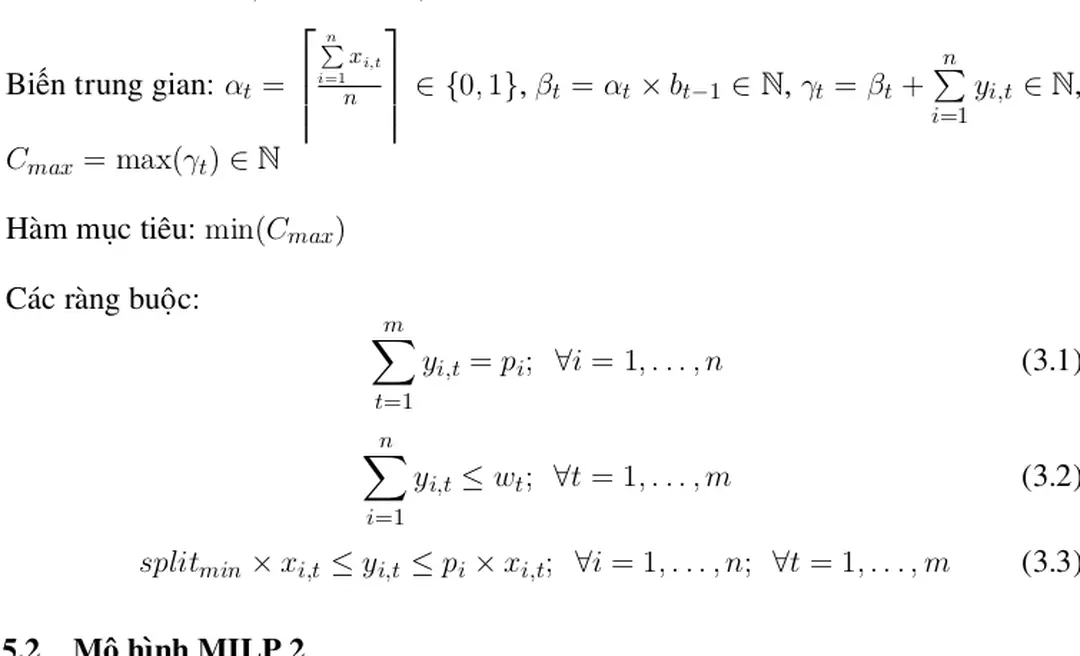


TÀI LIỆU CÙNG NGƯỜI DÙNG
-
128 5 0
-
209 6 2
-
41 5 0
-
59 0 0
-
46 2 0
-
88 9 0
TÀI LIỆU LIÊN QUAN
-
44 720 0
-
31 37 0
-
7 750 0
-
18 2,8K 10
-
128 1K 0
-
31 54 0
-
36 226 1
-
19 952 0