TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI VIỆN ĐIỆN BÁO CÁO BÀI TẬP LỚN Đề tài Tìm hiểu về robot Puma 500 Giảng viên hướng dẫn PGS TS Nguyễn Phạm Thục Anh Nhóm sinh viên thực hiện 6 Lớp 129135 Năm học 2021 – 2022 Mục lục Nội dung báo cáo Sinh viên thực hiện Trang 1 Giới thiệu về Robot Puma 500, các ứng dụng trong công nghiệp, kết cấu cơ khí, các thông số kĩ thuật cơ bản Nguyễn Hoàng long 20181611 1 3 2 Tính toán động học thuận vị trí Robot Xây dựng chương trình phần mềm trên matlab để nhập liệu và hiệ.
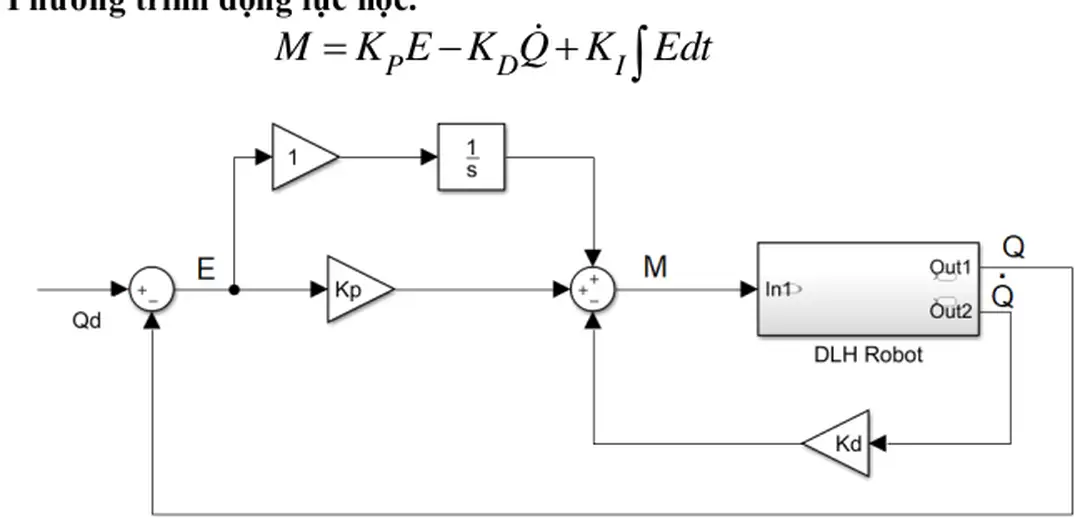
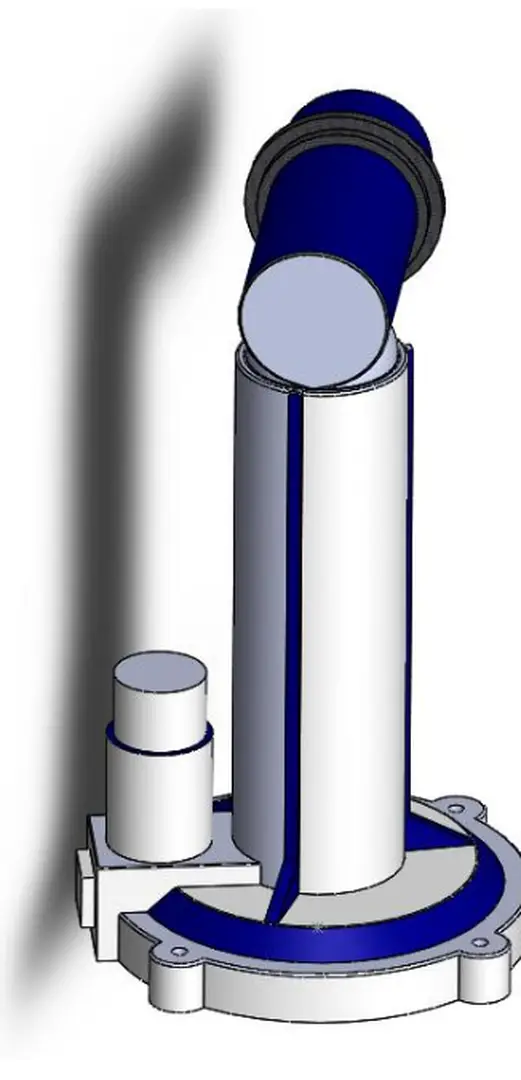
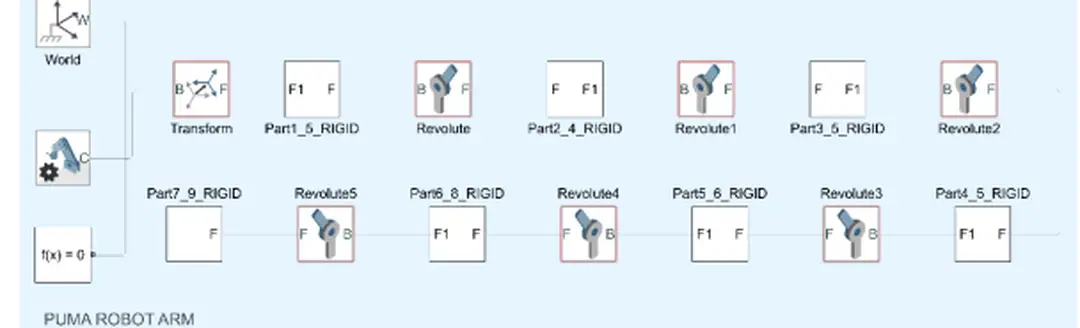
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI VIỆN ĐIỆN - - BÁO CÁO BÀI TẬP LỚN Đề tài: Tìm hiểu robot Puma 500 Giảng viên hướng dẫn: PGS TS Nguyễn Phạm Thục Anh Nhóm sinh viên thực hiện: Lớp:129135 Năm học 2021 – 2022 Mục lục Nội dung báo cáo Giới thiệu Robot Puma 500, ứng dụng công nghiệp, kết cấu khí, thơng số kĩ thuật Sinh viên thực Trang 1-3 Nguyễn Hồng long 20181611 Tính tốn động học thuận vị trí Hồng Minh Đức 20181402 Robot Xây dựng chương trình phần mềm matlab để nhập liệu Nguyễn Hương Ly 20181637 thị kết Phạm Yến linh 20181581 3-9 Tính tốn ma trận Jacoby (thơng qua Hồng Minh Đức 20181402 jH) viết chương trình matlab 9-15 Nguyễn Hương Ly 20181637 Phạm Yến linh 20181581 Tính tốn động học đảo vị trí Robot Tống Xuân Sơn 20186313 15-22 Vi Hồng Nam 20181671 Nguyễn Văn Sang 20181725 Thiết kế quỹ đạo chuyển động cho Tống Xuân Sơn 20186313 khớp robot theo quỹ đạo bậc 23 Vi Hồng Nam 20181671 Xây dựng mơ hình động lực học cho đối tượng Toolbox Simscape/Matlab Nguyễn Văn Sang 20181725 Đoàn Diễm Quỳnh 20181390 Đỗ Quang Cường 20160534 24-34 Giới thiệu Robot Puma 500, ứng dụng cơng nghiệp, kết cấu khí, thơng số kĩ thuật 1.1 Giới thiệu robot Puma 500 PUMA( P rogramable U niversal M achine for A ssembly P rogramable U niversal for A rm) Được phát triển Giáo sư người Mĩ Victor David Scheinman công ty robot tiên phong Unimation Vào năm 1980 dựa thiết kế mà ông phát minh học Đại học Stanford Puma 500 dịng seri đạt tới độ cao gần 2m sử dụng ngơn ngữ lập trình val Thiết kế gồm phần chính: cánh tay hệ thống điều khiển Chúng kết nối với hai dây cáp lớn nhiều dây dẫn Khi hai dây cáp sử dụng, dây dẫn truyền lực đến động servo phanh dây thứ hai mang phản hồi vị trí cho khớp trở lại hệ Unimate 500 PUMA (1983), thiết bị điều thống điều khiển Máy tính điều khiển thiết bị đầu cuối máy tính khiển dựa kiến trúc LSI-11 giống với máy tính PDP11 Hệ thống có chương trình khởi động cơng cụ gỡ lỗi tải chip ROM Hệ điều hành tải từ nhớ ngồi thơng qua cổng nối tiếp, thường từ đĩa mềm Bộ điều khiển chứa nguồn servo, bảng xử lý phản hồi tương tự kỹ thuật số, hệ thống truyền động servo 1.2 Thông số kĩ thuật AXES revolute axes Configuaration degrees of freedom Dive Elictric DC servomotors Power Requirement 110-130 VAC, 50-60Hz,1500 Watts Repeatability ± 0.1 mm Maximum static load 25 N Maximum Straight Line Velocity 51cm/sec Reach 86,6 cm to the wrist 92.2 cm to the flange Weight 54.4 kg Các thơng số khí tính inch Joint Axis of Maximum angle rotation of rotation Joint 1Waist Z 320° Joint 2- X Shoulder 250° Joint 3Elbow X 270° Joint4Y Wrist Rotation 300° 1.3 Ứng dụng Puma 500 Puma 500 dùng dây truyền sản suất gắp di chuyển vật co khối lượng nhẹ dây truyền sản xuất đồ uống, dung vẽ kĩ thuật với tốc độ độ xác cao cịn nhiều ứng dụng khác y2mate.com - Food y2mate.com application with Puma 500 robot_480p.mp4Drawing with the PUMA Robot Arm_480p.mp4 Video ứng dụng robot puma 500 Tính tốn động học thuận vị trí Robot Xây dựng chương trình phần mềm matlab để nhập liệu thị kết 2.1 Phương pháp Danevit – Hartenberg (D-H) Bước 1: Xác định số khớp nối Robot - n khớp (i=1->n): khớp quay + tịnh tiến - (n+1) nối: 0->n - nối cố định - nối n gắn với khâu tác động cuối - khớp i nối nối (i-1) i Bước 2: Khai báo hệ trục tọa độ nối OiXiYiZi (i=0->n) ➢ Xác định trục Zi - Khớp (i+1) tịnh tiến: Zi trục mà theo khớp (i+1) trượt - Khớp (i+1) quay: Zi trục mà xung quanh khớp (i+1) quay ➢ Xác định trục Xi - Trường hợp 1: Zi-1 Zi chéo nhau: Xi đường vng góc chung Zi-1 Zi Hình1: Zi-1 Zi chéo - Trường hợp 2: Zi-1 // Zi Hình Zi-1 // Zi Trường hợp 3: Zi-1 X Zi Hình Zi-1 cắt Zi Bước 3: Xác định thông số động học nối Các tham số+ ai: chiều dài nối, ai>=0 + αi: góc vặn nối i + di: độ lệch với nối (i-1) + qi: góc quay nối i Bước 4: Xác định ma trận Ai T ii −1 = Ai = Rot(Z,θi)Trans(Z,di)Trans(Xi,ai)Rot(X,ai) cos i − sin i 0 1 0 1 0 sin cos i 0 0 0 0 0 i = 0 1 0 cos i 0 sin i 0 0 0 d i 0 0 0 0 0 0 0 0 1 − sin i cos i cos i cos i sin i 0 1 − sin i cos i cos i sin i = sin i sin i − cos i sin i cos i cos i sin i di Bước 5: Tìm T 0n T 0n = A 10 A 12 …A nn −1 n x0 ny = n z s x0 s 0y s z0 a x0 a 0y a z0 p x0 p 0y p z0 Chú ý rằng, ma trận chuyển vị từ hệ i đến hệ i-1 hàm biến khớp i (nếu khớp thứ i khớp quay) d i (nếu khớp thứ i khớp trượt) Một cách tổng quát, quy tắc Denavit – Hartenberg cho phép tổ hợp ma trận chuyển vị riêng rẽ thành mà trận chuyển vị nhất, biểu diễn vị trí hướng khâu n so với khâu sở 2.2 Phân tích động học Robot PUMA 2.2.1 Động học thuận vị trí Hình 2.2 Gắn hệ trục tọa độ hệ tọa độ trung gian cho Robot Áp dụng quy tắc Denavit – Hartenberg ta thu bảng D-H, biểu diễn bảng: Bảng 2.1 Bảng thông số D-H Khâu tác động 𝜶𝒊 𝒂𝒊 𝒅𝒊 𝜽𝒊 -90 0 t1 a2 -d2 t2 90 a3 t3 -90 d4 t4 90 0 t5 0 d6 t6 Các ma trận Ai tính tốn dựa theo cơng thức: Ai = Rot ( Z ,i )Trans ( Z , d i )Trans ( X i , ) Rot ( X , i ) ci s Ai = i 0 0 Ta thu kết quả: c s A = 0 0 1 c s A = 0 0 4 −c s c c s 1 1 −c s c c s 4 4 s s − s c c 1 1 s s − s c c 4 a c a s d a c a s d 1 1 4 −c i s i c i c i s i 4 4 4 c s A = 0 0 s i s i − s i c i c i 2 c s A = 0 0 −c s c c s 2 c i s i di 2 −c s c c s 5 5 Từ ma trận sở ta tính tốn ma trận vị trí 𝑇06 2 2 s s − s c c 2 s s − s c c 𝑛𝑥 𝑛 𝑦 𝑇60 = 𝐴1 𝐴2 𝐴3 𝐴4 𝐴5 𝐴6 = [ 𝑛𝑧 5 𝑜𝑥 𝑜𝑦 𝑜𝑧 2 2 5 a c a s d a c a s d 5 5 𝑎𝑥 𝑎𝑦 𝑎𝑧 5 c s A = 0 0 3 c s A = 0 0 𝑝𝑥 𝑝𝑦 ] 𝑝𝑧 6 −c s c c s 3 3 6 6 3 3 −c s c c s s s −s c c s s −s c c 6 3 3 Trong đó: nx = − 𝑠𝑖𝑛(𝑡6) ∗ (𝑐𝑜𝑠(𝑡4) ∗ 𝑠𝑖𝑛(𝑡1) + 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4)) − 𝑐𝑜𝑠(𝑡6) ∗ (𝑐𝑜𝑠(𝑡5) ∗ (𝑠𝑖𝑛(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4) − 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡1) ∗ 𝑐𝑜𝑠(𝑡4)) + 𝑠𝑖𝑛(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡1) ∗ 𝑠𝑖𝑛(𝑡5)) ny = 𝑠𝑖𝑛(𝑡6) ∗ (𝑐𝑜𝑠(𝑡1) ∗ 𝑐𝑜𝑠(𝑡4) − 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑠𝑖𝑛(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4)) + 𝑐𝑜𝑠(𝑡6) ∗ (𝑐𝑜𝑠(𝑡5) ∗ (𝑐𝑜𝑠(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4) + 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡4) ∗ 𝑠𝑖𝑛(𝑡1)) − 𝑠𝑖𝑛(𝑡2 + 𝑡3) ∗ 𝑠𝑖𝑛(𝑡1) ∗ 𝑠𝑖𝑛(𝑡5)) ny = 𝑠𝑖𝑛(𝑡6) ∗ (𝑐𝑜𝑠(𝑡1) ∗ 𝑐𝑜𝑠(𝑡4) − 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑠𝑖𝑛(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4)) + 𝑐𝑜𝑠(𝑡6) ∗ (𝑐𝑜𝑠(𝑡5) ∗ (𝑐𝑜𝑠(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4) + 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡4) ∗ 𝑠𝑖𝑛(𝑡1)) − 𝑠𝑖𝑛(𝑡2 + 𝑡3) ∗ 𝑠𝑖𝑛(𝑡1) ∗ 𝑠𝑖𝑛(𝑡5)) nz = 𝑠𝑖𝑛(𝑡2 + 𝑡3) ∗ 𝑠𝑖𝑛(𝑡4) ∗ 𝑠𝑖𝑛(𝑡6) − 𝑐𝑜𝑠(𝑡6) ∗ (𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑠𝑖𝑛(𝑡5) + 𝑠𝑖𝑛(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡4) ∗ 𝑐𝑜𝑠(𝑡5)) ox = 𝑠𝑖𝑛(𝑡6) ∗ (𝑐𝑜𝑠(𝑡5) ∗ (𝑠𝑖𝑛(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4) − 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡1) ∗ 𝑐𝑜𝑠(𝑡4)) + 𝑠𝑖𝑛(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡1) ∗ 𝑠𝑖𝑛(𝑡5)) − 𝑐𝑜𝑠(𝑡6) ∗ (𝑐𝑜𝑠(𝑡4) ∗ 𝑠𝑖𝑛(𝑡1) + 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4)) oy = 𝑐𝑜𝑠(𝑡6) ∗ (𝑐𝑜𝑠(𝑡1) ∗ 𝑐𝑜𝑠(𝑡4) − 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑠𝑖𝑛(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4)) − 𝑠𝑖𝑛(𝑡6) ∗ (𝑐𝑜𝑠(𝑡5) ∗ (𝑐𝑜𝑠(𝑡1) ∗ 𝑠𝑖𝑛(𝑡4) + 𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡4) ∗ 𝑠𝑖𝑛(𝑡1)) − 𝑠𝑖𝑛(𝑡2 + 𝑡3) ∗ 𝑠𝑖𝑛(𝑡1) ∗ 𝑠𝑖𝑛(𝑡5)) oz = 𝑠𝑖𝑛(𝑡6) ∗ (𝑐𝑜𝑠(𝑡2 + 𝑡3) ∗ 𝑠𝑖𝑛(𝑡5) + 𝑠𝑖𝑛(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡4) ∗ 𝑐𝑜𝑠(𝑡5)) + 𝑠𝑖𝑛(𝑡2 + 𝑡3) ∗ 𝑐𝑜𝑠(𝑡6) ∗ 𝑠𝑖𝑛(𝑡4) a c a s d a c a s d 6 6 6 2.Thiết kế quỹ đạo không gian khớp Chọn hai điểm A, B không gian làm việc, biết tọa độ (Px,P y, Pz) hướng khâu thao tác Thiết kế quỹ đạo chuyển động từ A đến B Theo toán động học ta xác định biến khớp 𝜃1 , 𝜃2 , 𝜃3 , 𝜃4 , 𝜃5, 𝜃6 A B Chọn quỹ đạo thiết kế hàm đa thức bậc theo thời gian sau: 𝜃𝑖 (𝑡) = 𝑎𝑖 + 𝑏𝑖 𝑡 + 𝑐𝑖 𝑡 + 𝑑𝑖 𝑡 Với: i =1÷6 tương ứng với biến khớp Ta hệ phương trình sau: 𝜃1 (𝑡) = 𝑎1 + 𝑏1 𝑡 + 𝑐1 𝑡 + 𝑑1 𝑡 𝜃2 (𝑡) = 𝑎2 + 𝑏2 𝑡 + 𝑐2 𝑡 + 𝑑2 𝑡 𝜃3 (𝑡) = 𝑎3 + 𝑏3 𝑡 + 𝑐3 𝑡 + 𝑑3 𝑡 𝜃4 (𝑡) = 𝑎4 + 𝑏4 𝑡 + 𝑐4 𝑡 + 𝑑4 𝑡 𝜃5 (𝑡 ) = 𝑎5 + 𝑏5 𝑡 + 𝑐5 𝑡 + 𝑑5 𝑡 {𝜃6 (𝑡 ) = 𝑎6 + 𝑏6 𝑡 + 𝑐6 𝑡 + 𝑑6 𝑡 Giả sử thời gian robot từ điểm A đến điểm B t(s) vân tốc điểm Từ ta có hệ phương trình: 𝜃𝑖 (𝐴) = 𝑎𝑖 𝜃𝑖 (𝐵) = 𝑎𝑖 + 𝑏𝑖 𝑡 + 𝑐𝑖 𝑡 + 𝑑𝑖 𝑡 𝜃𝑖 (𝐴) = 𝑏𝑖 = {𝜃𝑖 (𝐵) = 𝑏𝑖 + 2𝑐𝑖 𝑡 + 3𝑑𝑖 𝑡 = 𝑎𝑖 = 𝜃𝑖 (𝐴) 𝑏𝑖 = 3[𝜃𝑖 (𝐵) − 𝜃𝑖 (𝐴)] 𝑐𝑖 = 𝑡2 2[𝜃𝑖 (𝐵) − 𝜃𝑖 (𝐴)] 𝑑 = { 𝑖 𝑡3 Giả sử robot PUMA cần dịch chuyển từ vị trí A) đến điểm B 6s tương ứng với tọa độ khớp A(0,0,0,0,0) đến B(90,30,0,0,90) (góc 𝜃𝑖 – góc quay khớp, đơn vị ‘độ’) Ta suy hệ số phương trình quỹ đạo cho khâu là: 21 𝑎1 = 𝜃1 (𝐴) = 𝑏1 = 3[𝜃1 (𝐵) − 𝜃1 (𝐴)] 3[90 − 0] 𝑐1 = = = 7.5 𝑡2 62 2[𝜃1 (𝐵) − 𝜃1 (𝐴)] −2[90 − 0] 𝑑 = = = −0.833 { 𝑡3 63 Khi ta có phương trình quỹ đạo vị trí, vận tốc, gia tốc theo thời gian : 𝜃1 (𝑡) = 7,5 𝑡 − 0,833 𝑡 𝜃̇1 (𝑡) = 7,5.2 𝑡 − 0,833.3 𝑡 𝜃̈1 (𝑡) = 7,5.2 − 0,833.3.2 𝑡 Đồ thị quỹ đạo chuyển động bậc khớp 1: 22 5.Điều khiển chuyển động cho robot theo thuật toán PID 5.1 Phương trình động lực học M = K P E − K DQ + K I Edt Hình Sơ đồ cấu trúc điều khiển PID 5.2 Thiết kế điều khiển PID Với tham số Kp=450, Ki=600, Kd=20 Dựa vào đặc điểm ảnh hưởng tham số tới đáp ứng đầu mô hình ta chỉnh định tham số cho đàu bám giá trị đặt đạt số tiêu chí độ độ thời gian đáp ứng sai lệch tĩnh 23 6.XÂY DỰNG MƠ HÌNH ROBOT TRÊN SIMMECHANICS/MATLAB 6.1 Mơ hình Robot 1.1 Mơ hình 3D Robot SolidWork Mơ hình Robot PUMA 560 khớp thiết kế Solidworks hình Hình Khớp robot 24 Hình Khớp robot Hình Khớp robot 25 Hình Khớp robot Hình Khớp robot Hình Khớp robot 26 Hình Robot PUMA hồn chỉnh 6.2 Sơ đồ khối Robot Matlab Simulink - Để tiến hành mô Robot sau vẽ SolidWorks dựa Toolbox Simscape Matlab, cần cài đặt “Simscape Multibody Link” Ở ta chọn Simscape Multibody Link 6.1 dành cho R2019a (Matlab2019a) - Sau download hai file “smlink.r2019a.win64.zip” “install_addon.m”, ta mở Matlab để tiến hành cài đặt Mở thư mục chứa file gõ lệnh “install_addon('smlink.r2019a.win64.zip')” để tiến hành cài dặt - Khi trình cài đặt kết thúc, ta mở Solidworks lên click vào mục Add-Ins → Chọn Simscape Multibody Link - Sau mục tool Tool chọn Simscape Multibody Link → Export→ Simscape Multibody… để tiến hành xuất Solidworks dạng file xml 27 - Sau hoàn thành xuất file, ta mở Matlab, mở thư mục chứa file xml, cửa sổ Command gõ lệnh Smimport để xuất file xml sang file slx Simulink - Cuối robot Puma sau chuyển sang Simulink ta mơ hình sau: Hình Robot PUMA Model Simulink Tiếp theo ta thiết kế điều khiển cho robot PUMA 6.3 Bộ điều khiển PID Hình 10 Sơ đồ điều khiển PID Mơ hình biểu diễn dựa phương trình sau 𝑀 = 𝐾𝑝 𝐸 − 𝐾𝐷 𝑄 + 𝐾𝐼 ∫ 𝐸 𝑑𝑡 Trong đó: E sai lệch 𝑄𝑑 (Q đặt) hay 𝑄𝑟𝑒𝑓 (Q reference) hình: Với 𝐸 = 𝑄𝑑 − 𝑄 𝑄𝑑 Vị trí biến khớp mong muốn 𝑄𝑑 = [45 90 120 90 135 180]𝑇 𝐾𝑝 , 𝐾, 𝐾𝐼 số điều khiển PID 28 Hình 10 Sơ đồ Bộ điều khiển PID cho khớp Hình 11 Sơ đồ Bộ điều khiển PID cho Robot PUMA 29 Hình 12 PUMA RBOT ARM với Bộ điều khiển PID thiết kế 30 1.4 Đồ thị đáp ứng đầu khớp Hình 13 Đồ thị vị trí đáp ứng đầu khớp Hình 14 Đồ thị vị trí đáp ứng đầu khớp 31 Hình 15 Đồ thị vị trí đáp ứng đầu khớp Hình 16 Đồ thị vị trí đáp ứng đầu khớp 32 Hình 17 Đồ thị vị trí đáp ứng đầu khớp Hình 18 Đồ thị vị trí đáp ứng đầu khớp 33 Hình 19 Sơ đồ cấu trúc PID Simulink 34 35BÀI TẬP LỚN KỸ THUẬT ROBOT: Tìm hiểu về robot Puma 500
37
15
0
THÔNG TIN TÀI LIỆU
Thông tin cơ bản
| Tiêu đề | Tìm hiểu về robot Puma 500 |
|---|---|
| Tác giả | Nguyễn Hoàng Long, Hoàng Minh Đức, Nguyễn Hương Ly, Phạm Yến Linh, Tống Xuân Sơn, Vi Hồng Nam, Nguyễn Văn Sang, Đoàn Diễm Quỳnh, Đỗ Quang Cường |
| Người hướng dẫn | PGS. TS Nguyễn Phạm Thục Anh |
| Trường học | Trường Đại Học Bách Khoa Hà Nội |
| Thể loại | báo cáo |
| Năm xuất bản | 2021 – 2022 |
| Thành phố | Hà Nội |
| Định dạng | |
|---|---|
| Số trang | 37 |
| Dung lượng | 1,95 MB |
Nội dung
Ngày đăng: 25/06/2022, 17:01
HÌNH ẢNH LIÊN QUAN













TỪ KHÓA LIÊN QUAN
TÀI LIỆU CÙNG NGƯỜI DÙNG
-
38 21 2
-
37 27 0
-
35 13 1
-
32 5 0
-
45 32 1
-
55 14 2
TÀI LIỆU LIÊN QUAN
-
43 7 0
-
72 22 2
-
45 0 0
-
31 10 0
-
70 8 0
-
61 4 0
-
37 15 0
-
67 44 0