Giáo trình : GIẢI TÍCH MẠNG part 7 potx

Giáo trình : GIẢI TÍCH MẠNG part 10 potx
... tuyến tính. 10 1.4.2. Hạng của ma trận. 10 1.5. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH. 10 CHƯƠNG 2: GIẢI PHƯƠNG TRÌNH VI PHÂN BẰNG PHƯƠNG PHÁP SỐ. 12 2.1. GIỚI THIỆU. 12 2.2. GIẢI PHƯƠNG TRÌNH VI ... diện biểu diễn hình ảnh về các ma trận mạng GIẢI TÍCH MẠNG Trang 142 MỤC LỤC Lời nói đầu . CHƯƠNG 1: ĐẠI SỐ MA TRẬN ỨNG DỤNG TRONG GIẢI TÍCH MẠNG. 4 1.1. ĐỊNH NGHĨA V...
Ngày tải lên: 27/07/2014, 16:21

Giáo trình : GIẢI TÍCH MẠNG part 9 pps
... máy l : GIẢI TÍCH MẠNG Trang 130 T R : Là hằng số thời gian của bộ điều chỉnh. K A : Là hệ số khuyếch đại của bộ khuếch đại. T A : Là hằng số thời gian của bộ khuyếch đại. K E : Là ... Với: E s : Là điện áp được ghi trong lịch trình tính ở đơn vị tương đối. iii E 0 : Là điện áp lấy ra của bộ khuếch đại trong đơn vị tương đối trước sự nhiễu loạn....
Ngày tải lên: 27/07/2014, 16:21
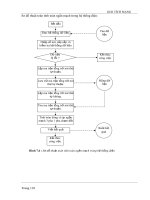
Giáo trình : GIẢI TÍCH MẠNG part 8 doc
... đó l : me P θθ . 2 = (8. 2) Tần số f trong mỗi giây của chu kỳ l : 60 . 2 nP f = (8. 3) Từ phương trình (8. 2) và (8. 3) góc lệch độ điện tính bằng radian l : me n f θθ . 60 = (8. 4) Vị ... GIẢI TÍCH MẠNG Trang 111 Phương pháp biến đổi Euler và Runge - Kuta được thực hiện để giải các phương trình vi phân trong việc nghiên cứu tính ổn định của quá trình quá độ...
Ngày tải lên: 27/07/2014, 16:21

Giáo trình : GIẢI TÍCH MẠNG part 7 potx
... phương trình (7. 32) dùng dòng điện vòng hiện tại. Dòng nhánh bù cây có thể tính toán từ phương trình (7. 27) và điện áp nút, sau đó có thể xác định từ phương trình (7. 28). Trong phương trình (7. 33) ... chạm đất l : Dòng 3 pha và điện áp nút ngắn mạch thu được bằng sự thay thế từ phương trình (7. 22) vào trong phương trình (7. 15), (7. 17) và (7. 19). Dòng ngắn...
Ngày tải lên: 27/07/2014, 16:21

Giáo trình : GIẢI TÍCH MẠNG part 6 doc
... ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ s n d T b ba s n I I I ZZ ZZ V V V M M M M LLLLL M M L M 11 (6. 27) Vì V s biết trước nên ta tìm I s từ (n -1) phương trình đầu như sau: Rút từ (6. 27) và chuyển về nghịch đảo Z d ta c : GIẢI TÍCH MẠNG Trang 96 Với là tổng ... dụng trong giải tích mạng. Với trường hợp gi...
Ngày tải lên: 27/07/2014, 16:21

Giáo trình : GIẢI TÍCH MẠNG part 5 doc
... Từ phương trình (5. 13) ta c : lilNuïtNuïtNuït IZIZE r r r += (5. 21) V : i, j = 1, 2, m (5. 22) 0 =+= lllNuïtljl IZIZe rr Giải I l từ phương trình (5. 22) và thế vào (5. 21 ): Nuï t ll ljil NuïtNuït I Z ZZ ZE r r r r ). . ( ... rspqrspl yy ,, rr = pqpqplpl yy ,, = Nên: plpl rsrspl pl y vy v , , .1 ∑ + −= r r (5. 19) Thế lần lượt phương trình (5. 19), (5. 6)...
Ngày tải lên: 27/07/2014, 16:21

Giáo trình : GIẢI TÍCH MẠNG part 4 ppt
... các nút. Vì vậy có tỉ lệ tương ứng 1:1 giữa các đường và các nút. A b .K t = 1 (4. 3) Do đ : K t = A b -1 (4. 4) GIẢI TÍCH MẠNG Trang 47 4. 3 .4. Ma trận vết cắt cơ bản B. Liên hệ ... thêm của graph trình bày trên hình 4. 5 là ma trận B ˆ như sau: GIẢI TÍCH MẠNG Trang 45 eia j ji ,2,10 4 0 == ∑ = n 4 0 1 2 3 e Đ = 1 7 6 5 4...
Ngày tải lên: 27/07/2014, 16:21

Giáo trình : GIẢI TÍCH MẠNG part 3 doc
... (3. 1) và (3. 2) theo x ta c : dx dI z dx Vd . 2 2 = (3. 3) dx dV y d x Id . 2 2 = (3. 4) Thế (3. 1) và (3. 2) vào (3. 3) và (3. 4) ta c : Vyz dx Vd 2 2 = (3. 5) Iyz d x Id 2 2 = (3. 6) Giải ... ) 22 1 (/) 2 . 1( 2 1 ; 2 11 22 1 /) 2 . 1( Y Z ZY B A Y Y B Y Y Z ZY B D Y RR RSSR SS +−=+−=−= =−=−= +=+== (3. 33) Các tham số này có thể tính trực tiếp từ sơ đồ hình 3. 4 vi...
Ngày tải lên: 27/07/2014, 16:21

Giáo trình : GIẢI TÍCH MẠNG part 2 pps
... 0,8 125 0,0 622 4 0,01874 0,0 629 1 0,018 72 0,875 0,0 722 6 0, 020 04 0,01873 0,175 0,875 0,0 722 7 0, 020 04 0,9375 0,0 822 9 0, 021 34 0,0 829 4 0, 021 32 1,000 0,09359 0, 022 60 0, 021 33 0 ,20 0 1,000 0,09360 0, 022 60 ... 0, 022 29 0,10475 0, 022 30 1,000 0,11590 0, 021 99 0, 022 30 0 ,22 5 1,000 0,11590 0, 021 99 1,0000 0, 126 90 0, 021 67 0, 126 74 0, 021 68 1,000 0,13758 0, 021...
Ngày tải lên: 27/07/2014, 16:21

Giáo trình : GIẢI TÍCH MẠNG part 1 doc
... .b i2 2j + + a iq .b qj Ví d : 2 212 1 211 213 211 31 2 212 1 211 212 211 21 2 212 1 211 211 211 11 22 21 1 211 babababa babababa babababa bb bb ++ ++ ++ = 32 31 22 21 1 211 . aa aa aa BA = x B.A Phép ... định thức. 22 21 1 211 || aa aa A = Giải phương trình (1. 1) bằng phương pháp định thức ta c : 211 22 211 212 122 222 12 1 1 aaaa kaka A ak ak x...
Ngày tải lên: 27/07/2014, 16:21

Giáo trình giải tích 2 part 9 potx
... 1, √ 3) ax 2 +2bxy + cy 2 + dx + ey + f =0 (x 0 ,y 0 ,z 0 ) (2, −1, 2) S 1 : x 2 + y 2 + z 2 =9 S 2 : z = x 2 + y 2 − 3. R 3 S 1 : x 2 + y 2 + z 2 =3 S 2 : x 3 + y 3 + z 3 =3. S 1 ,S 2 (1, 1, 1) R 3 S 1 : ... 1, 1) R 3 S 1 : ax 2 + by 2 + cz 2 =1 S 2 : xyz =1. a, b, c S 1 ,S 2 c(t)=(3t 2 ,e t ,t+ t 2 ) t =1 c(t)=(2cost, 2sint, t) t = π /2 f(x, y, z...
Ngày tải lên: 01/08/2014, 00:20

Giáo trình giải tích 2 part 7 doc
... x 2 ≤ y ≤ b a a 2 − x 2 } v(E)= a −a ( b a √ a 2 −x 2 − b a √ a 2 −x 2 dy)dx = a −a 2 b a a 2 − x 2 dx =2ab(arcsin x a + x 2 a a 2 − x 2 )| a −a = πab. n>1 P 0 V 1 , ··· ,V k T δ = ... ≤ z ≤ h 2 (x, y)} f C C C f(x, y, z)dxdydz = Ω ( h 2 (x,y) h 1 (x,y) f(x, y, z)dz)dxdy E = { x 2 a 2 + y 2 b 2 ≤ 1} E Ox [−a, a] C x = {y : − b a a...
Ngày tải lên: 01/08/2014, 00:20

Giáo trình giải tích 2 part 1 potx
... R ∞ k=0 x k , ∞ k =1 x k k , ∞ k =1 x k k 2 1 ln 2 = 1 − 1 2 + 1 3 − 1 4 + 1 5 −···+ ( 1) n +1 n +1 + R n π 4 =1 1 3 + 1 5 − 1 7 + 1 9 −···+ ( 1) n 2n +1 + R n R n O( 1 n ) f x 0 f(x)= ∞ k=0 a k (x ... +1 =ln (1+ x) |x| < 1 1 1+ x 2 = 1 1 − (−x 2 ) =1 x 2 + x 4 − x 6 + ···= ∞ k=0 ( 1) k x 2k , |x| < 1 arctan x = x − x 3 3 + x...
Ngày tải lên: 01/08/2014, 00:20

Giáo trình giải tích 1 part 8 potx
... ∞ k =1 1 k 2 =1+ 1 2 2 + 1 3 2 + ··· S n =1+ 1 2 2 + 1 3 2 + ···+ 1 n 2 ≤ 1+ 1 1.2 + 1 2.3 + ···+ 1 (n 1) n ≤ 1+ 1 1 − 1 2 + 1 2 − 1 3 + ···+ 1 (n 1) − 1 n < 2 − 1 n ∞ k=0 ( 1) k =1 1+ 1− 1+ ··· ... = 1 2 − 1 4 + 1 6 − 1 8 + 1 10 − 1 12 + ··· =0+ 1 2 − 0 − 1 4 +0+ 1 6 − 0 − 1 8 + ··· ln 2 + 1 2 ln 2 = (1 + 0) + (− 1 2...
Ngày tải lên: 01/08/2014, 00:20

Giáo trình giải tích 1 part 7 docx
... = ϕ(b) ϕ(a) f(x)dx x π 1 0 dx 1+ x 2 =arctanx| 1 0 = π 4 1 − q n +1 1 − q =1+ q + q 2 + ···+ q n q = −x 2 1 1+x 2 =1 x 2 + x 4 − x 6 + ···+( 1) n x 2n + R n , R n = ( 1) n +1 x 2n+2 1+ x 2 π 4 =1 1 3 + 1 5 − 1 6 + ... = a 1 <a 2 < ···<a n = b ≤ +∞ b a f(x)dx = c 1 a 1 f(x)dx + a 2 c 1 f(x)dx + ···+ c n 1 a n 1 f(x)dx + a n c n 1 f(x)d...
Ngày tải lên: 01/08/2014, 00:20