Phân tích ứng xử của dầm composite sử dụng lý thuyết đàn hồi phi cục bộ

TỔNG QUAN

Đặt vấn đề

Vật liệu composite là một loại vật liệu hỗn hợp được tạo thành từ hai hoặc nhiều loại vật liệu khác nhau, với cấu trúc phụ thuộc vào sự kết hợp giữa vật liệu nền và vật liệu gia cường dạng hạt hoặc sợi Nhờ vào những ưu điểm vượt trội của các thành phần, vật liệu composite mang lại nhiều lợi ích hơn so với vật liệu truyền thống và hiện đang được ứng dụng hiệu quả trong các lĩnh vực kỹ thuật như hàng không, cơ khí, hàng hải, y khoa và xây dựng.

Dầm composite chức năng có cấu trúc nhiều lớp, và sự thay đổi đột ngột về đặc tính và thành phần vật liệu giữa các lớp gây ra hiện tượng tập trung ứng suất lớn Tuy nhiên, hiện tượng này có thể được giảm thiểu đáng kể để cải thiện hiệu suất của kết cấu.

Hình 1.1: Phân loại vật liệu composite [43]

Vật liệu composite chức năng (Functionally Graded Material - FGM) là loại vật liệu đặc biệt với đặc trưng vật liệu thay đổi liên tục, giúp cải thiện khả năng chịu lực của kết cấu FGM được chế tạo từ một loại vật liệu hỗn hợp có sự biến đổi liên tục trong các thành phần cấu tạo, thường được ứng dụng trong các điều kiện làm việc khắc nghiệt như lá chắn nhiệt của tàu vũ trụ, cấy ghép sinh học, và các bộ phận động cơ Việc sử dụng vật liệu FGM trong kết cấu xây dựng mở ra tiềm năng ứng dụng lớn nhằm gia cường độ bền cho các công trình.

Hình 1.3: Một số hình ảnh về ứng dụng của vật liệu FGM trong tự nhiên [44,45]

Việc ứng dụng hiệu quả vật liệu composite trong nhiều ngành công nghiệp yêu cầu phát triển các lý thuyết dầm composite để dự báo hành vi tĩnh, ổn định và dao động Nhiều nghiên cứu gần đây đã áp dụng các phương pháp và cách tiếp cận khác nhau Đặc biệt, lý thuyết đàn hồi phi cục bộ Eringer và lý thuyết biến dạng cắt bậc cao quasi-3D, với sự chú ý đến biến dạng pháp tuyến, đã được phát triển và chứng minh tính phù hợp trong phân tích ứng xử của các kết cấu ở cấp độ vi mô và nano.

Nghiên cứu cho thấy ứng suất không chỉ phụ thuộc vào biến dạng tại một điểm mà còn liên quan đến biến dạng tại tất cả các điểm trong môi trường liên tục, và đáp ứng của kết cấu phụ thuộc vào kích thước vật liệu thành phần Mặc dù đã có nhiều tác giả nghiên cứu về dầm đồng nhất, nhưng số lượng nghiên cứu về ứng xử của dầm composite chức năng sử dụng lý thuyết đàn hồi phi cục bộ và lý thuyết biến dạng cắt bậc cao dạng quasi-3D, bao gồm cả biến dạng pháp tuyến, vẫn còn hạn chế Do đó, đề tài này được chọn để nghiên cứu sâu hơn.

Tổng quan tình hình nghiên cứu

Vật liệu chức năng FGM là sự kết hợp của hai vật liệu với tỉ lệ nhất định, nhằm đạt được chức năng mong muốn theo mục đích sử dụng Tính chất của vật liệu này biến đổi từ bề mặt này sang bề mặt khác, giúp giảm thiểu sự tập trung ứng suất Kết cấu từ vật liệu chức năng FGM được ứng dụng rộng rãi trong nhiều lĩnh vực như cơ khí, xây dựng dân dụng, hàng không, công nghiệp hạt nhân và ô tô Ngoài ra, vật liệu chức năng FGM còn được áp dụng trong các thiết bị nano và micro.

Trong những năm gần đây, nghiên cứu về hiệu ứng kích thước vật liệu thành phần đã gia tăng, với nhiều mô hình được phát triển cho dầm composite chức năng Lý thuyết đàn hồi phi cục bộ Eringen cho rằng ứng suất phụ thuộc vào biến dạng tại tất cả các điểm trong môi trường liên tục, dẫn đến sự phát triển của các lý thuyết dầm như lý thuyết dầm phi cục bộ Euler-Bernoulli và Timoshenko Các lý thuyết này kết hợp với lý thuyết dầm Euler-Bernoulli (EBT) và lý thuyết dầm Timoshenko (TBT), cũng như lý thuyết biến dạng cắt bậc cao (HBT), để đánh giá hiệu ứng biến dạng pháp tuyến Lý thuyết EBT, mặc dù đơn giản, không tính đến hiệu ứng biến dạng cắt và chỉ phù hợp cho dầm mỏng, trong khi lý thuyết TBT có khả năng xem xét hiệu ứng này nhưng yêu cầu các điều kiện phức tạp hơn.

Bài viết này đề cập đến 4 hệ số hiệu chỉnh cắt nhằm điều chỉnh sự phân bố không đồng đều của ứng suất cắt qua chiều dày dầm Trong lý thuyết dầm HBT, hiệu ứng biến dạng cắt được xem xét mà không cần sử dụng hệ số hiệu chỉnh cắt, nhờ vào sự thay đổi bậc cao của trường chuyển vị dọc trục hoặc sự chuyển vị trong và ngoài mặt phẳng.

Lý thuyết HBT nghiên cứu chuyển vị trong mặt phẳng tiết diện dầm thông qua hàm bậc cao cho chuyển vị theo phương tiếp tuyến, nhưng không tính đến chuyển vị theo phương pháp tuyến Để khắc phục hạn chế này, lý thuyết quasi-3D đã được phát triển nhằm giải quyết vấn đề chuyển vị theo phương pháp tuyến trong tiết diện dầm.

Nghiên cứu về ứng xử tĩnh, dao động và ổn định của dầm nano đã được thực hiện bởi Reddy, sử dụng các lý thuyết dầm khác nhau cùng lý thuyết phi cục bộ Wang và Liew đã áp dụng lý thuyết dầm phi cục bộ Euler-Bernoulli và Timoshenko để nghiên cứu ứng xử uốn dầm Ansari và Sahmani sử dụng lý thuyết dầm cổ điển để phân tích tĩnh và ổn định của dầm nano Murmu và Pradhan đã phân tích ổn định của ống nano carbon trong môi trường đàn hồi bằng lý thuyết dầm Timoshenko và phương pháp DQM.

Bài viết phân tích dao động tự do của ống nano thông qua các lý thuyết biến dạng cắt dầm khác nhau Wang và cộng sự đã áp dụng lý thuyết đàn hồi phi cục bộ Eringen cùng với lý thuyết dầm Timoshenko để nghiên cứu ứng xử uốn của dầm vi mô và nano.

Một cách tiếp cận khác để nghiên cứu hiệu ứng kích thước vật liệu thành phần là áp dụng lý thuyết đàn hồi phi cục bộ và môi trường nhiệt nhằm phân tích hành vi của dầm chức năng Các nghiên cứu đã chỉ ra rằng việc phân tích phi tuyến của dầm chức năng có thể thực hiện thông qua lý thuyết chênh lệch biến dạng phi cục bộ, cùng với lý thuyết ứng suất tương tác hiệu chỉnh, mang lại cái nhìn sâu sắc về ứng xử của vật liệu trong các điều kiện khác nhau.

Mục tiêu đề tài

Mục tiêu của nghiên cứu này là phân tích ứng xử của dầm FGM thông qua lý thuyết biến dạng cắt bậc cao quasi-3D, bao gồm cả biến dạng pháp tuyến và lý thuyết đàn hồi phi cục bộ, nhằm làm rõ các vấn đề liên quan đến đặc điểm ứng xử của dầm trong điều kiện khác nhau.

 Phân tích hiệu ứng kích thước vật liệu thành phần đến các đáp ứng tĩnh, dao động và ổn định dầm FGM

Phân tích ứng xử của dầm FGM dưới tác động của tải trọng cơ nhiệt và độ ẩm, bao gồm cả biến dạng pháp tuyến và không bao gồm biến dạng pháp tuyến, cho thấy sự khác biệt rõ rệt trong kết quả Nghiên cứu này so sánh với các nghiên cứu trước đó, cung cấp cái nhìn sâu sắc về ảnh hưởng của các yếu tố này đến hiệu suất của dầm FGM.

Phương pháp nghiên cứu

Các nghiên cứu và kết quả đạt được đều được áp dụng các phương pháp nghiên cứu sau:

 Sử dụng lý thuyết biến dạng cắt bậc cao dạng quasi-3D có kể đến biến dạng pháp tuyến

 Lý thuyết đàn hồi phi cục bộ nhằm kể đến hiệu ứng tỉ lệ kích thước vật liệu

 Sử dụng nguyên lý Hamilton nhằm rút ra phương trình chuyển động

Sử dụng lời giải Navier để giải quyết ba bài toán cơ bản: dầm chịu uốn, bài toán ổn định và bài toán dao động tự do dưới tác động của tải trọng cơ học Bên cạnh đó, thực hiện phân tích bài toán ổn định và dao động tự do khi chịu ảnh hưởng của nhiệt độ và độ ẩm, cả trong trường hợp tuyến tính lẫn phi tuyến.

 Sử dụng lời giải Ritz để phân tích bài toán dao động tự do với các điều kiện biên khác nhau

Tính mới đề tài

Tính mới của đề tài thể hiện trong các điểm sau:

Chưa có nghiên cứu nào thực hiện trên dầm FGM sử dụng đồng thời lý thuyết đàn hồi phi cục bộ và lý thuyết biến dạng cắt bậc cao dạng quasi-3D, trong đó có tính đến biến dạng pháp tuyến cùng với các điều kiện biên khác nhau.

Nội dung nghiên cứu

Các nội dung chính sau sẽ được thực hiện trong đề tài:

 Phân tích bài toán dầm chịu uốn trong đó độ võng cực đại được tính toán và so sánh với nghiên cứu trước

 Phân tích bài toán dao động tự do trong đó tần số dao động và mode dao động được phân tích và đánh giá

 Phân tích bài toán ổn định trong đó lực ổn định tới hạn được phân tích và đánh giá

Bài viết phân tích dao động tự do và ổn định dưới tác động của tải trọng nhiệt độ và độ ẩm, bao gồm cả các yếu tố tuyến tính và phi tuyến Tần số dao động và lực ổn định tới hạn được đánh giá kỹ lưỡng, giúp hiểu rõ hơn về ảnh hưởng của các yếu tố môi trường đến hệ thống.

 Phân tích dao động tự do bằng phương pháp Ritz với các điều kiện biên khác nhau trong đó tần số dao động được phân tích và đánh giá

CƠ SỞ LÝ THUYẾT

Giới thiệu

Vật liệu chức năng FGM là sự kết hợp của hai vật liệu với tỉ lệ nhất định nhằm đạt được chức năng mong muốn theo mục đích sử dụng Tính chất của vật liệu này thay đổi từ bề mặt này sang bề mặt khác, giúp giảm thiểu sự tập trung ứng suất Các kết cấu làm từ vật liệu chức năng FGM được ứng dụng rộng rãi trong nhiều lĩnh vực như cơ khí, xây dựng dân dụng, hàng không, công nghiệp hạt nhân và ô tô Đặc biệt, vật liệu chức năng FGM còn được ứng dụng trong các thiết bị nano và micro.

Trong những năm gần đây, hiệu ứng kích thước vật liệu thành phần đã trở thành một chủ đề quan trọng trong nghiên cứu kết cấu Nghiên cứu thực nghiệm đã chỉ ra rằng ứng xử của dầm composite chức năng bị ảnh hưởng bởi kích thước vật liệu thành phần Để đánh giá hiệu ứng này, nhiều mô hình đã được phát triển, trong đó lý thuyết đàn hồi phi cục bộ Eringen là một trong những lý thuyết tiêu biểu Lý thuyết này cho rằng ứng suất không chỉ phụ thuộc vào biến dạng tại một điểm mà còn vào biến dạng tại tất cả các điểm trong môi trường liên tục Dựa trên lý thuyết này, các mô hình dầm như lý thuyết dầm phi cục bộ Euler-Bernoulli và Timoshenko đã được phát triển Lý thuyết dầm Euler-Bernoulli là lý thuyết đơn giản nhất nhưng không tính đến hiệu ứng biến dạng cắt, do đó chỉ phù hợp cho dầm mỏng Ngược lại, lý thuyết dầm Timoshenko xem xét hiệu ứng biến dạng cắt nhưng cần hệ số hiệu chỉnh cắt để điều chỉnh phân bố ứng suất Cuối cùng, lý thuyết dầm biến dạng cắt bậc cao không yêu cầu hệ số hiệu chỉnh nhờ vào sự thay đổi bậc cao của trường chuyển vị.

Lý thuyết HBT nghiên cứu chuyển vị trong mặt phẳng tiết diện dưới dạng hàm bậc cao cho chuyển vị theo phương tiếp tuyến, nhưng bỏ qua chuyển vị theo phương pháp tuyến Để khắc phục hạn chế này, lý thuyết quasi-3D đã được phát triển nhằm giải quyết vấn đề chuyển vị theo phương pháp tuyến trong tiết diện dầm.

Mặc dù một số mô hình dầm đã được phát triển dựa trên lý thuyết đàn hồi phi cục bộ để nghiên cứu ứng xử của dầm composite chức năng, nhưng nghiên cứu về dầm FGM sử dụng lý thuyết biến dạng cắt bậc cao dạng quasi-3D vẫn còn hạn chế Chương này sẽ trình bày cơ sở lý thuyết cho phân tích bài toán này, dựa trên lý thuyết dầm biến dạng cắt bậc cao, lý thuyết đàn hồi phi cục bộ và nguyên lý Hamilton để rút ra các phương trình chuyển động.

Cơ sở lý thuyết

Xem xét dầm FGM có chiều dài L, chiều rộng tiết diện b và chiều cao tiết diện h như Hình 2.1

Hình 2.1: Kích thước hình học của dầm chức năng [41]

2.2.1 Các đặc tính vật liệu dầm FGM

Dầm chức năng có các đặc tính vật liệu như mô đun đàn hồi Young (E), mô đun trượt (G), hệ số Poisson (ν) và mật độ khối lượng (ρ) được giả định thay đổi liên tục theo chiều dày Các chỉ số m và c đại diện cho các pha vật liệu kim loại và gốm tương ứng.

Mô đun đàn hồi của vật liệu, ký hiệu là P(z), được xác định theo công thức P(z) = P - P V(z) + P Trong đó, các yếu tố liên quan bao gồm mật độ khối lượng ρ(z), hệ số Poisson ν(z), hệ số giãn nở nhiệt α(z) và hệ số giãn nở độ ẩm.

 của dầm FGM vi cấu trúc

Trong đó hàm mật độ thể tích vật liệu gốm V c đối với dầm FGM có dạng như sau:

  (2.2) trong đó p là tham số vật liệu thể hiện sự phân bố vật liệu theo chiều dày lớp thay đổi, p0

Các tính chất của vật liệu chịu nhiệt được biểu diễn dưới dạng nhiệt sau:

P T z H H T    H T H T H T (2.3) trong đó H H 0 ,  1 ,H H H 1 , 2 , 3 là các hệ số phụ thuộc nhiệt độ cho các vật liệu khác nhau

2.2.2 Sự phân bố nhiệt độ và độ ẩm

Nhiệt độ và độ ẩm được khảo sát ở trường hợp phân bố đều, thay đổi tuyến tính và thay đổi phi tuyến

Nhiệt độ và độ ẩm phân bố đều (UTR) được giả định không thay đổi theo chiều dày dầm, với sự gia tăng đồng đều từ nhiệt độ và độ ẩm ban đầu T C 0, 0 như đã được chỉ ra trong tài liệu [41].

C C 0 C (2.4b) trong đó T 0 , C 0 là nhiệt độ và độ ẩm tham chiếu

Nhiệt độ và độ ẩm tuyến tính (LTR): nhiệt độ và độ ẩm được giả thiết thay đổi tuyến tính theo chiều dày dầm được cho bởi [41]

C z  C C V C (2.5b) trong đó T c , T m , C c và C m lần lượt là nhiệt độ và độ ẩm của lớp trên, dưới dầm,

Nhiệt độ và độ ẩm phi tuyến (NLTR): nhiệt độ và độ ẩm được giả thiết thay đổi phi tuyến dạng cosin được cho bởi [42]

2.2.3 Lý thuyết dầm biến dạng cắt bậc cao và lý thuyết đàn hồi phi cục bộ

2.2.3.1 Lý thuyết dầm biến dạng cắt bậc cao

Trường chuyển vị của dầm được chọn như sau [41]:

3( , , ) ( , ) z ( , ) u x z t w x t g z w x t (2.7c) trong đó Hàm f(z) được chọn như sau [43]:

, u , w , w z là 4 biến tại mặt trung bình dầm cần xác định Các biến dạng khác không cho bởi:

Mối quan hệ ứng suất biến dạng:

2 x x y y z z yz yz xz xz xy xy

Nếu  y  xy  yz 0, phương trình (2.11) trở thành

Khi  z 0mối quan hệ ứng suất biến dạng cho bởi

Theo nguyên lý Hamilton phương trình chuyển động cho bởi:

    (2.16) trong đó  U ,  V ,  K lần lượt là năng lượng biến dạng, công thực hiện và động năng

Năng lượng biến dạng được cho bởi :

Sự thay đổi công của tải trọng ngoài dưới tác dụng tải trọng nén dọc trục

N 0và tải trọng ngang q, nhiệt độ và độ ẩm được cho bởi:

Sự thay đổi động năng được cho bởi:

(2.21) trong đó I I I J J K L L 0 , , 1 2 , 1 , 2 , 2 , 1 , 2 được xác định bởi:

Áp dụng nguyên lý Hamilton, kết hợp với sự thay đổi năng lượng biến dạng, công của tải trọng ngoài và động năng, phương trình cân bằng của dầm được xác định qua các biểu thức liên quan.

: x xx b xx t xx m xx x xx x z w M q N w N w N w I u I w I w J L w

2.2.3.2 Lý thuyết đàn hồi phi cục bộ

Theo lý thuyết đàn hồi phi cục bộ của Eringen phương trình cấu tạo được cho bởi [17]:

Trong phương trình (2.24), ứng suất toàn cục \( t_{ij} \) được xác định bởi toán tử Laplacian \( \nabla^2 \), với hệ số tỷ lệ chiều dài \( \mu = (e a_0)^2 \) phản ánh ảnh hưởng của quy mô nhỏ Ở đây, \( e_0 \) là mật độ các phần tử và \( a \) là khoảng cách giữa các phần tử Dựa vào phương trình (2.25), lý thuyết đàn hồi phi cục bộ cung cấp một phương trình ứng xử chính xác cho các hệ thống vật liệu.

Từ phương trình (2.9), (2.18), phương trình (2.25) ta được

Q  Q  A  w (2.26e) trong đó A B B D D H , , S , , S , S , K S , E S , F S , G S , A S được xác định bởi:

Từ phương trình (2.23) và (2.26) phương trình cân bằng của dầm được cho bởi các biểu thức sau

: xx xxx s xx s z x xx xxx xx x u Au Bw B E w I u I w J

: xxx xxxx s xxx s z xx xx xxxx t xxxx m xxxx t m xx xx xx xxx xxxx xx xxx z xx x xx x z w Bu Dw D F w q N w N w N w q N w N w N w I u I w I w J L w

: s xx s xxx s xx s z x s z x xx xxx xx x

Dựa trên lời giải Navier, trường lời giải (2.28) được giả thiết như sau:

(2.29) trong đó i 2  1,  n /L,  là tần số dao động riêng của dầm Tải trọng ngang cũng được phát triển thành chuỗi Fourier có dạng như sau:

 (2.30) trong đó Q n q 0 đối với tải trọng hình sin và 4 0 n

 đối với tải trọng phân bố đều.Từ phương trình (2.29) và (2.30) thế vào phương trình (2.28) rút ra được phương trình sau

Các thành phần của ma trận độ cứng K ij và ma trận khối lượng M ij được tính toán dựa trên độ cứng và khối lượng của dầm, cũng như số sóng n lan truyền Việc giải phương trình này giúp xác định chuyển vị, ứng suất, tần số dao động riêng và tải trọng ổn định tới hạn.

Ma trận K ij và ma trận khối lượng M ij được cho bởi

Lời giải của phương trình (2.32) giúp thu được độ võng, tần số dao động và lực ổn định tới hạn của dầm FGM Trong đó F là ngoại lực

2.3 Phương pháp lời giải Ritz

Lời giải Navier (2.29) chỉ áp dụng cho dầm đơn giản Để giải quyết bài toán với các điều kiện biên khác nhau, phương pháp Ritz là một lựa chọn hiệu quả Dựa trên phương pháp này, trường chuyển vị có thể được áp dụng để tìm ra giải pháp tối ưu cho các bài toán liên quan.

Trong bài viết này, phương trình (2.33d) mô tả tần số dao động với i² = -1 là đơn vị ảo Các giá trị cần xác định bao gồm u, w, j, θ, và w zj, trong khi ψ j (x) và φ j (x) là các hàm dạng tương ứng với từng điều kiện biên khác nhau Khi thay thế phương trình (2.34) vào phương trình (2.29) ở Chương 2, ta có thể thu được kết quả mong muốn.

(2.34) trong đó các thành phần của ma trận độ cứng K ij và ma trận khối lượng M ij được cho bởi

L L L L ij i j xxx ij i j xxxx i j xxxx i j xx

L L L L s s s s ij i j xx ij i j xxx ij i j xx i j

Lời giải của phương trình (3.3) giúp thu được tần số dao động của dầm FGM

Các hàm dạng và các điều kiện biên

Bảng 2.1: Các điều kiện biên

BCs Vị trí Giá trị

VÍ DỤ SỐ

Tổng quát

Các lý thuyết đã được phát triển sẽ được áp dụng để tính toán tần số dao động, lực ổn định tới hạn và độ võng của dầm composite chức năng.

Bài viết này trình bày các ví dụ tính toán bằng phần mềm Matlab nhằm hỗ trợ việc tính toán phức tạp và so sánh hiệu quả của lý thuyết biến dạng cắt bậc cao dạng quasi-3D với các điều kiện biên khác nhau Đồng thời, bài viết cũng kết hợp lý thuyết đàn hồi phi cục bộ để nghiên cứu các bài toán đã được các tác giả khác thực hiện, từ đó rút ra nhận xét và đánh giá về kết quả nghiên cứu.

Các ví dụ số bao gồm:

Bài toán 1: Tính toán tần số dao động của dầm FGM

Bài toán 2: Tính toán lực ổn định tới hạn của dầm FGM

Bài toán 3: Tính toán độ võng của dầm FGM

Bài toán 4: Tính toán tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm phân bố đều sử dụng lời giải Navier

Bài toán 5 : Tính toán tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm tuyến tính

Bài toán 6 : Tính toán tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm phi tuyến

Bài toán 7: Tính toán lực ổn định tới hạn của dầm FGM tác động nhiệt và độ ẩm phân bố đều sử dụng lời giải Ritz

Bài toán 8: Sử dụng lời giải giải tích tính toán tần số dao động của dầm FGM với điều kiện biên H-S

Bài toán 9: Sử dụng lời giải giải tích tính toán tần số dao động của dầm FGM với điều kiện biên C-C

Bảng 3.1: Thông số của dầm FGM

Tần số dao động được tính theo

Lực ổn định tới hạn được tính theo

 E I (4.2) Độ võng cực đại được tính theo ax 4

Bài toán 1 : Tính toán tần số dao động của dầm FGM

Dầm FGM với phía trên là Al2O3, ở dưới là Metal, không ảnh hưởng đến nhiệt độ và độ ẩm Thông số được cho trong Bảng 3.1

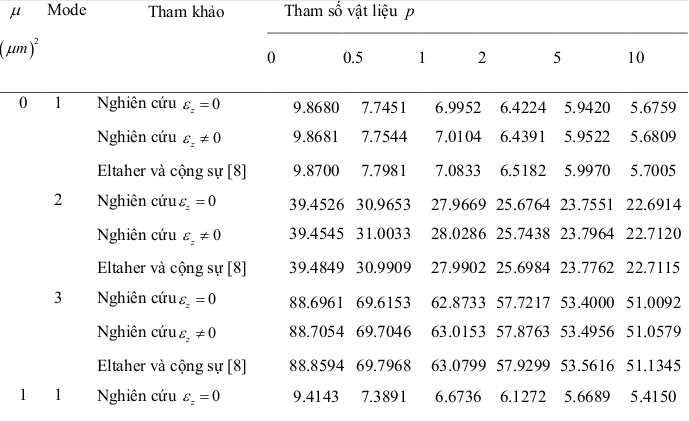
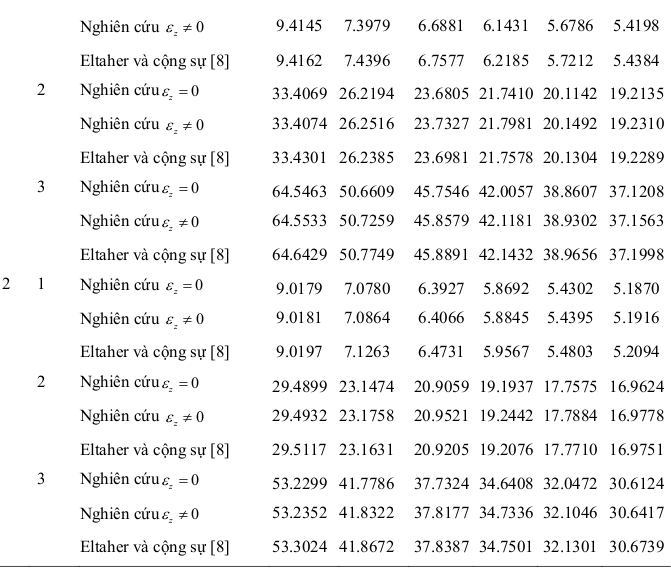
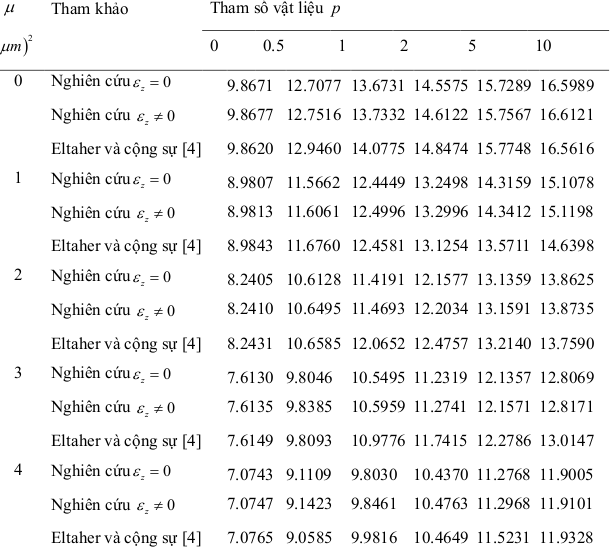
Bảng 3.2: Ảnh hưởng của tỉ số L/h, hệ số, tham số vật liệu p lên tần số dao động của dầm FGM L h / 0

 Mode Tham khảo Tham số vật liệu p

Dầm FGM với phía trên là Al 2 O 3 , ở dưới là SUS304, không ảnh hưởng đến nhiệt độ và độ ẩm Thông số được cho trong Bảng 3.1

Bảng 3.3: Ảnh hưởng của tỉ số L/h, hệ số, tham số vật liệu p lên tần số dao động của dầm FGM L h /

Nghiên cứu   z 0 9.4145 7.3979 6.6881 6.1431 5.6786 5.4198 Eltaher và cộng sự [8] 9.4162 7.4396 6.7577 6.2185 5.7212 5.4384

 Tham khảo Tham số vật liệu p

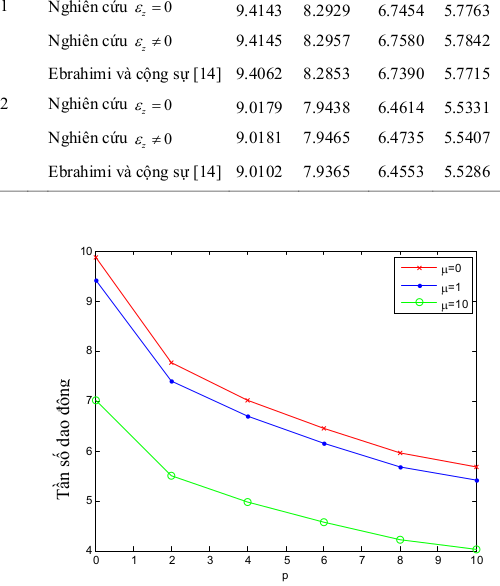
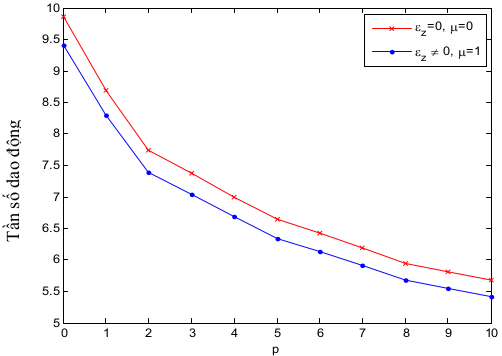
Hình 3.1: Ảnh hưởng của tham số p, hệ số  lên tần số dao động mode 1 có tính đến biến dạng cắt L/h0

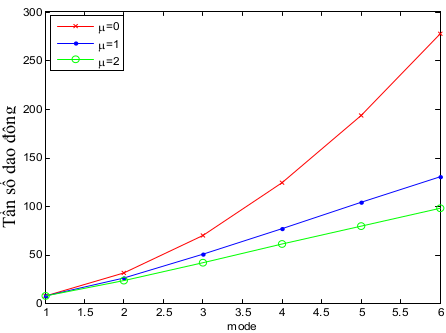
Hình 3.2: Ảnh hưởng của hệ số, lên 3 mode dao động có tính đến biến dạng cắt L/h0

Hình 3.3: Ảnh hưởng của hệ số , tham sốp lên tấn số dao động trong hai trường hợp có hoặc không có bến dạng cắt L/h0

Tần số dao độngTần số dao động

- Khi tăng tham số vật liệu và tăng hệ số phi cục bộ thì tần số dao động giảm dần trong mỗi mode dao động

- Tần số dao động sẽ tăng dần khi tăng mode dao động

- Tần số dao động có xét đến biến dạng cắt có kết quả lớn hơn khi không xét đến biến dạng cắt.

Bài toán 2 : Tính toán lực ổn định tới hạn của dầm FGM

Dầm FGM với phía trên là Al2O3, ở dưới là Metal, không ảnh hưởng đến nhiệt độ và độ ẩm Thông số được cho trong bảng 3.1.

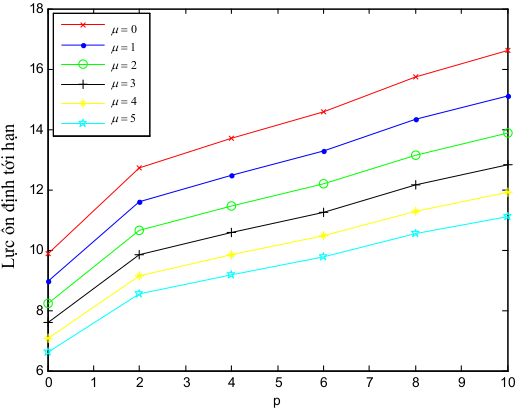
Bảng 3.4: Ảnh hưởng của hệ số , tham số p đến lực ổn định tới hạn của dầm FGM Tỉ lệ L/h0

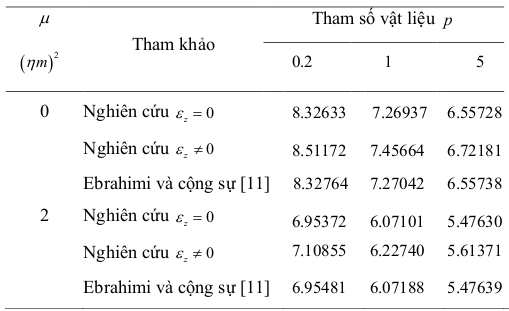
Dầm FGM với phía trên là Si3N4, ở dưới là SUS304, không ảnh hưởng đến nhiệt độ và độ ẩm Thông số được cho trong Bảng 3.1

Bảng 3.5: Ảnh hưởng của hệ số , tham số p đến lực ổn định tới hạn của dầm FGM Tỉ lệ L/h=5

Hình 3.4: Ảnh hưởng của hệ số, tham số plên lực ổn định tới hạn có tính đến biến dạng cắt L/h0

- Kết quả nghiên cứu là phù hợp với các nghiên cứu trước cho cả hai dầm mỏng và dầm dày

- Khi tăng tham số vật liệu p lực ổn định tới hạn tăng dần Khi  tăng thì lực ổn định tới hạn giảm dần

-Lực ổn định tới hạn có xét đến biến dạng cắt có kết quả lớn hơn khi không xét đến biến dạng cắt

- Hiệu ứng biến dạng pháp tuyến thể hiện rõ trong trường hợp dầm dày.

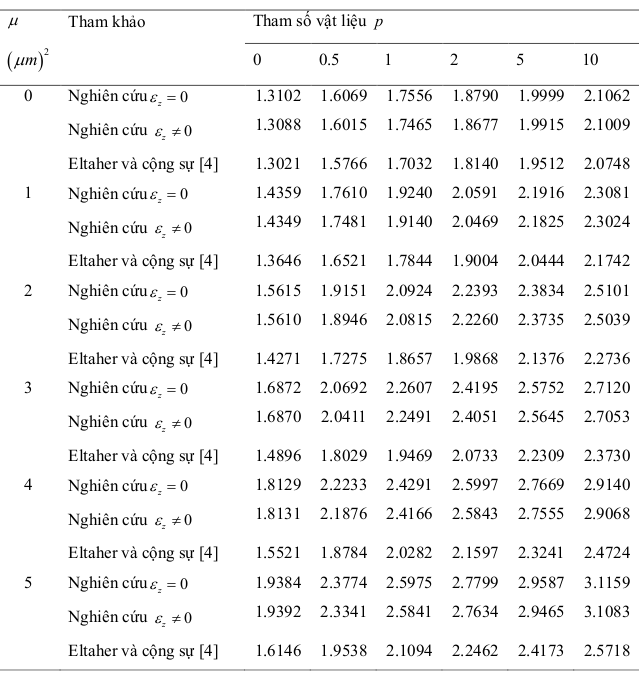
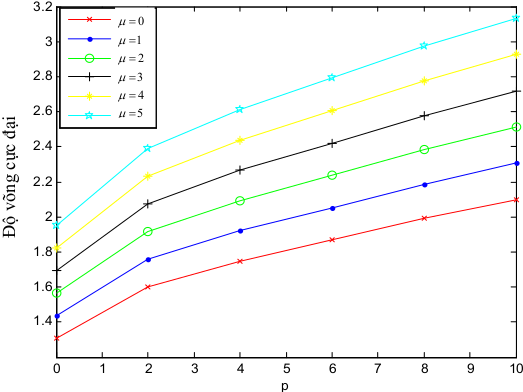
Bài toán 3: Tính toán độ võng của dầm FGM

Dầm FGM với phía trên là Al2O3, ở dưới là Metal, không ảnh hưởng đến nhiệt độ và độ ẩm Thông số được cho trong Bảng 3.1.

N c r ez#0 mu=0 mu=1 mu=2 mu=3 mu=4 mu=5

Lực ổn định tới hạn

Bảng 3.6: Ảnh hưởng của hệ số , tham số p đến độ võng cực đại của dầm FGM Tỉ lệ L/h

- Khi tăng tham số vật liệu và tăng hệ số phi cục bộ thì độ võng tăng dần

- Độ võng có xét đến biến dạng cắt có kết quả nhỏ hơn khi không xét đến biến dạng cắt

3.5 Bài toán 4: Tính toán tần số dao động của dầm FGM tác động nhiệt và độ ẩm phân bố đều sử dụng lời giải Navier

Dầm FGM với phía trên là Si3N4, ở dưới là SUS304 Thông số được cho trong Bảng 3.1.

Bảng 3.7: Tần số dao động của dầm FGM chịu tải phân bố đều dưới tác động nhiệt và độ ẩm, L/h

3.2 p u 3 ez#0 mu=0 mu=1 mu=2 mu=3 mu=4 mu=5 Độ võng cực đại

Hình 3.5: Ảnh hưởng của hệ số, tham số plên độ võng cực đại có tính đến biến dạng cắt L/h0

Hình 3.6: Ảnh hưởng của tham số p, nhiệt độ và độ ẩm lên tần số dao động khi  1, T 20có kể đến biến dạng cắt

0 Nghiên cứu  z  0 7.9680 5.9314 4.8450 7.4436 5.2167 4.0063 6.8673 4.3722 2.9180 Nghiên cứu   z 0 7.9730 5.9439 4.8525 7.4110 5.1629 3.9176 6.7899 4.2236 2.6499 Ebrahimi và Barati[17] 7.9681 5.9314 4.8450 7.4436 5.2167 4.0063 6.8673 4.3722 2.9180

1 Nghiên cứu  z  0 7.6017 5.6587 4.6222 7.0499 4.9041 3.7334 6.4384 3.9937 2.5299 Nghiên cứu  z  0 7.6064 5.6706 4.6295 7.0150 4.8454 3.6371 6.3552 3.8287 2.2137 Ebrahimi và Barati[17] 7.6018 5.6588 4.6222 7.0499 4.9041 3.7334 6.4384 3.9937 2.5299

2 Nghiên cứu   z 0 7.2817 5.4205 4.4277 6.7035 4.6269 3.4892 6.0570 3.6476 2.1527 Nghiên cứu   z 0 7.2862 5.4319 4.4346 6.6663 4.5634 3.3852 5.9679 3.4646 1.7689 Ebrahimi và Barati[17] 7.2817 5.4205 4.4277 6.7035 4.6269 3.4892 6.0570 3.6476 2.1527

Hình 3.7: Ảnh hưởng của nhiệt độ và độ ẩm lên tần số dao động khi

  có kể đến biến dạng cắt

- Khi chưa có sự ảnh hưởng của nhiệt độ và độ ẩm; tăng tham số vật liệu, hệ số phi cục bộ thì tần số dao động giảm dần

- Khi có ảnh hưởng của nhiệt độ và độ ẩm; tăng tham số vật liệu, hệ số phi cục bộ thì tần số dao động giảm dần

- Tần số dao động có ảnh hưởng của nhiệt độ và độ ẩm nhỏ hơn khi không ảnh hưởng của nhiệt độ và độ ẩm

Tần số dao động, khi xem xét đến biến dạng cắt cùng với ảnh hưởng của nhiệt độ và độ ẩm, sẽ cho kết quả thấp hơn so với trường hợp không tính đến biến dạng cắt.

3.6 Bài toán 5: Tính toán tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm tuyến tính

Dầm FGM với phía trên là Si 3 N 4 , ở dưới là SUS304 Thông số được cho trong Bảng 3.1.

Bảng 3.8: Tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm tuyến tính L/h

0 Nghiên cứu   z 0 7.8812 5.8495 4.7673 7.6632 5.5622 4.3967 7.4344 5.2556 3.9880 Nghiên cứu  z  0 7.8802 5.8551 4.7669 7.6477 5.5441 4.3572 7.4031 5.2108 3.9005 Ebrahimi và Barati[17] 7.8817 5.8491 4.7664 7.6651 5.5617 4.3962 7.4365 5.2519 3.9832

- Khi tăng tham số vật liệu, hệ số phi cục bộ thì tần số dao động giảm dần

Tần số dao động, khi xem xét ảnh hưởng của biến dạng cắt cùng với nhiệt độ và độ ẩm, thường cho kết quả thấp hơn so với khi không tính đến biến dạng cắt.

3.7 Bài toán 6: Tính toán tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm phi tuyến

Bảng 3.9: Tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm phi tuyến L/h

Hình 3.8: Ảnh hưởng nhiệt độ lên tần số dao động khi chịu tải phân bố đều, tuyến tính, phi tuyến có xét đến biến dạng pháp tuyến

Tần số dao động có tính đến biến dạng cắt, cùng với ảnh hưởng của nhiệt độ và độ ẩm phi tuyến, thường cho kết quả thấp hơn so với khi không xem xét biến dạng cắt.

Khi nhiệt độ và độ ẩm tăng lên, tần số dao động chịu tải phân bố đều sẽ nhỏ hơn tần số dao động chịu tải theo nhiệt độ và độ ẩm, cả tuyến tính lẫn phi tuyến.

3.8 Bài toán 7: Tính toán lực ổn định tới hạn của dầm FGM tác động nhiệt và độ ẩm phân bố đều sử dụng lời giải Ritz

Bảng 3.10: Lực ổn định tới hạn của dầm FGM chịu tải phân bố đều dưới tác động nhiệt và độ ẩm L/h

- Khi tăng tham số vật liệu, hệ số phi cục bộ thì lực ổn định tới hạn giảm dần

Lực ổn định tới hạn, khi xem xét biến dạng cắt và ảnh hưởng của nhiệt độ cùng độ ẩm phân bố đều, cho kết quả nhỏ hơn so với trường hợp không tính đến biến dạng cắt.

3.9 Bài toán 8: Sử dụng lời giải giải tích tính toán tần số dao động của dầm FGM với điều kiện biên H-S

Dầm FGM với phía trên là Al2O3, ở dưới là Metal không ảnh hưởng của nhiệt độ và độ ẩm Thông số được cho trong Bảng 3.1

Bảng 3.11: Ảnh hưởng của tỉ số L/h, hệ số, tham số vật liệu p lên tần số dao động của dầm FGM L h /  100

Denta T,Denta C=0,0 Denta T,Denta C ,0 Denta T,Denta C@,0

Hình 3.9: Ảnh hưởng của tham số p, nhiệt độ và độ ẩm lên lực ổn định tới hạn khi L h/ 20, 2

Bảng 3.12: Ảnh hưởng của tỉ số L/h, hệ số, tham số vật liệu p lên tần số cơ bản của dầm FGM L h /  20

- Tần số dao động giải bằng lời giải giải tích có kết quả giống như lời giải Navier

Khi tăng tham số vật liệu và hệ số phi cục bộ, tần số dao động sẽ giảm dần trong mỗi mode dao động Ngược lại, tần số dao động có xu hướng tăng lên khi mode dao động được tăng.

- Tần số dao động có xét đến biến dạng cắt có kết quả lớn hơn khi không xét đến biến dạng cắt

3.10 Bài toán 9: Sử dụng lời giải giải tích tính toán tần số dao động của dầm FGM với điều kiện biên C-C

Dầm FGM với phía trên là Al 2 O 3 , ở dưới là Metal không ảnh hưởng của nhiệt độ và độ ẩm Thông số được cho trong Bảng 3.1

Bảng 3.13: Ảnh hưởng của tỉ số L/h, hệ số, tham số vật liệu p lên tần số cơ bản của dầm FGM với phía trên là Al2O3, ở dưới là Metal L h /  20

Dầm FGM với phía trên là Al2O3, ở dưới là SUS304 không ảnh hưởng của nhiệt độ và độ ẩm Thông số được cho trong Bảng 3.1

Bảng 3.14: Ảnh hưởng của tỉ số L/h, hệ số, tham số vật liệu p lên tần số cơ bản của dầm FGM với phía trên là Al 2 O 3 , ở dưới là SUS304, L h /  20

- Tần số cơ bản sẽ giảm dần khi tăng tham số vật liệu, hệ số phi cục bộ

- Tần số cơ bản có kể đến biến dạng cắt lớn hơn khi không kể đến biến dạng cắt

Bài toán 5 : Tính toán tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm tuyến tính

Dầm FGM với phía trên là Si 3 N 4 , ở dưới là SUS304 Thông số được cho trong Bảng 3.1.

Bảng 3.8: Tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm tuyến tính L/h

Tần số dao động, khi xem xét biến dạng cắt và ảnh hưởng của nhiệt độ cũng như độ ẩm, thường cho kết quả thấp hơn so với trường hợp không tính đến biến dạng cắt.

Bài toán 6 : Tính toán tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm phi tuyến

Bảng 3.9: Tần số dao động của dầm FGM dưới tác động nhiệt và độ ẩm phi tuyến L/h

Hình 3.8: Ảnh hưởng nhiệt độ lên tần số dao động khi chịu tải phân bố đều, tuyến tính, phi tuyến có xét đến biến dạng pháp tuyến

Tần số dao động được điều chỉnh khi xem xét biến dạng cắt, ảnh hưởng của nhiệt độ và độ ẩm phi tuyến, thường có giá trị nhỏ hơn so với trường hợp không tính đến biến dạng cắt.

Khi nhiệt độ và độ ẩm tăng, tần số dao động chịu tải phân bố đều sẽ nhỏ hơn tần số dao động chịu tải nhiệt cũng như độ ẩm, cả trong trường hợp tuyến tính và phi tuyến.

Bài toán 7: Tính toán lực ổn định tới hạn của dầm FGM chịu tải phân bố đều dưới tác động nhiệt và độ ẩm sử dụng lời giải Ritz

Bảng 3.10: Lực ổn định tới hạn của dầm FGM chịu tải phân bố đều dưới tác động nhiệt và độ ẩm L/h

- Khi tăng tham số vật liệu, hệ số phi cục bộ thì lực ổn định tới hạn giảm dần

Lực ổn định tới hạn, khi tính đến biến dạng cắt và ảnh hưởng của nhiệt độ cũng như độ ẩm phân bố đều, sẽ cho kết quả nhỏ hơn so với trường hợp không xem xét biến dạng cắt.

Bài toán 8: Sử dụng lời giải giải tích tính toán tần số dao động của dầm FGM với điều kiện biên H-S

Dầm FGM với phía trên là Al2O3, ở dưới là Metal không ảnh hưởng của nhiệt độ và độ ẩm Thông số được cho trong Bảng 3.1

Bảng 3.11: Ảnh hưởng của tỉ số L/h, hệ số, tham số vật liệu p lên tần số dao động của dầm FGM L h /  100

Denta T,Denta C=0,0 Denta T,Denta C ,0 Denta T,Denta C@,0

Hình 3.9: Ảnh hưởng của tham số p, nhiệt độ và độ ẩm lên lực ổn định tới hạn khi L h/ 20, 2

Bảng 3.12: Ảnh hưởng của tỉ số L/h, hệ số, tham số vật liệu p lên tần số cơ bản của dầm FGM L h /  20

- Tần số dao động giải bằng lời giải giải tích có kết quả giống như lời giải Navier

Khi tăng tham số vật liệu và hệ số phi cục bộ, tần số dao động trong mỗi mode sẽ giảm dần Ngược lại, tần số dao động sẽ tăng khi tăng mode dao động.