Đăng nhập

Hãy chọn một cách để đăng nhập

Facebook Google Zalo

Hoặc tiếp tục với email

Nhớ mật khẩu

Chưa có tài khoản? Đăng ký

Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết

43 39 0

Đang tải... (xem toàn văn)

Tài liệu hạn chế xem trước, để xem đầy đủ mời bạn chọn Tải xuống

1 / 43 trang

THÔNG TIN TÀI LIỆU

thuvienhoclieu com thuvienhoclieu com CHUYÊN ĐỀ TAM GIÁC ĐỒNG DẠNG Bài 1 Cho ABC nhọn, các đường cao BD và CE cắt nhau tại H, CMR HD Từ H kẻ Khi đó (1) Tương tự (2) Cộng (1) và (2) theo vế ta được Bài 2 Cho BHC có tù, Vẽ BE vuông góc với CH tại E và CD vuông góc với BH tại D CMR HD Kẻ => (1) Tương tự ta có => (2) Cộng (1) và (2) theo vế ta được VT Bài 3 Cho ABC có góc A bằng 1200, AD là đường phân giác CMR HD Kẻ là tam giác đều có (đpcm) Bài 4 Cho A’, B’, C’ nằm trên các cạnh BC, AC, AB của ABC,[.]

Ngày đăng: 23/05/2022, 23:59

Xem thêm:

HÌNH ẢNH LIÊN QUAN

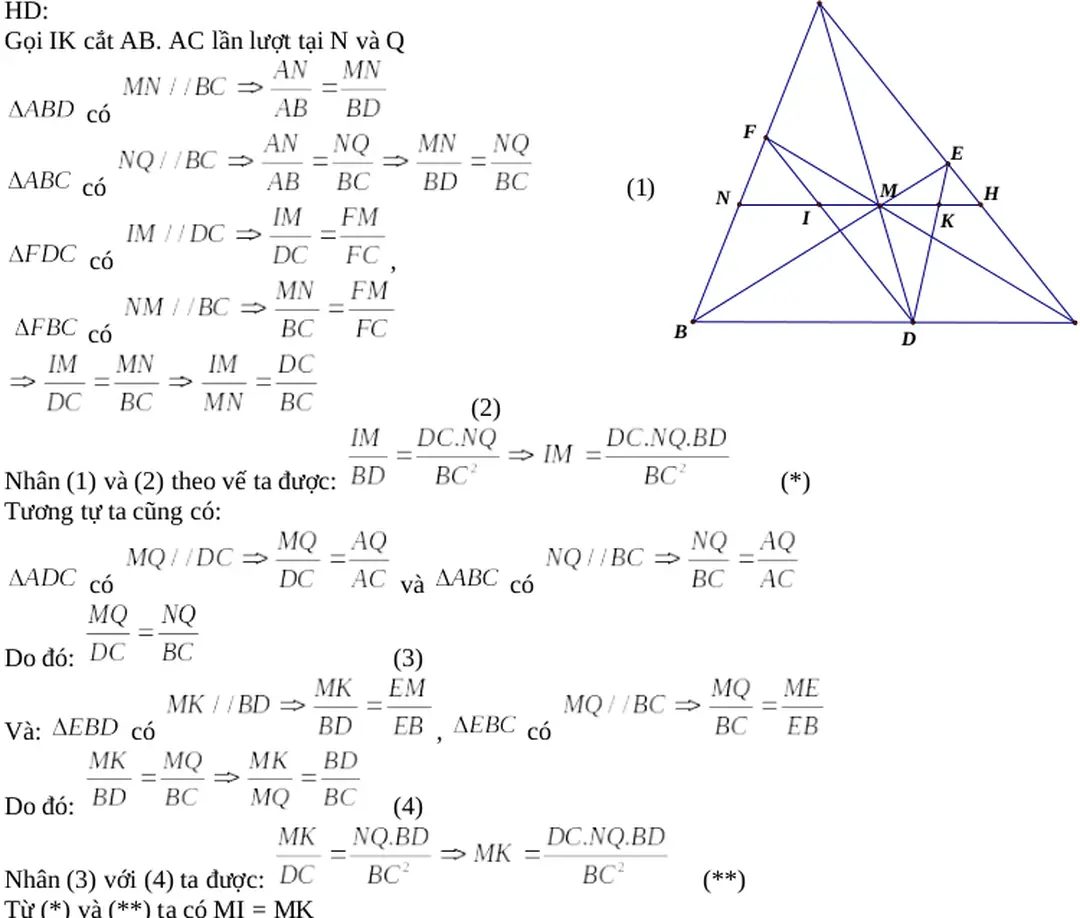
 => HGOK là hình bình hành => J là trung điểm của HO => HJ=OJ - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — gt ; HGOK là hình bình hành => J là trung điểm của HO => HJ=OJ (Trang 10)

Bài 19: Cho hình thang ABCD (AB//CD) có BC=BD, Gọi H là trung điểm của CD, đường thẳng đi qua H cắt AC, AD lần lượt tại E và F, CMR: DBF EBC·· - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 19: Cho hình thang ABCD (AB//CD) có BC=BD, Gọi H là trung điểm của CD, đường thẳng đi qua H cắt AC, AD lần lượt tại E và F, CMR: DBF EBC·· (Trang 11)

=> Tứ giác BMCN là hình bình hành => - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — gt ; Tứ giác BMCN là hình bình hành => (Trang 12)

, CMR: ABCD là hình bình hành - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — l à hình bình hành (Trang 13)

Bài 27: Cho tam giác ABC vuông tại A, đường cao AH, I là trung điểm của AC ,F là hình chiếu củ aI trên BC, trên nửa mặt phẳng bờ là đường thẳng chứa AC, vẽ tia Cx vuông góc với AC cắt IF tại E, Gọi giao của AH, AE với BI theo thứ tự tại G và K - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 27: Cho tam giác ABC vuông tại A, đường cao AH, I là trung điểm của AC ,F là hình chiếu củ aI trên BC, trên nửa mặt phẳng bờ là đường thẳng chứa AC, vẽ tia Cx vuông góc với AC cắt IF tại E, Gọi giao của AH, AE với BI theo thứ tự tại G và K (Trang 15)

Bài 3 5: Cho hình vuông ABCD, Gọi M, N theo thứ tự là các trung điểm của các cạnh AB, AD và P là giao điểm của BN, CM - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 3 5: Cho hình vuông ABCD, Gọi M, N theo thứ tự là các trung điểm của các cạnh AB, AD và P là giao điểm của BN, CM (Trang 20)

Bài 38: Cho hình vuông ABCD, gọi O là giao của hai đường chéo, lấy G trên BC, H trên CD sao cho - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 38: Cho hình vuông ABCD, gọi O là giao của hai đường chéo, lấy G trên BC, H trên CD sao cho (Trang 21)

Bài 40: Cho hình vuông ABCD, trên BC lấy E sao cho 3 - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 40: Cho hình vuông ABCD, trên BC lấy E sao cho 3 (Trang 22)

Bài 42: Cho hình vuông ABCD, trên AB lấy điểm M, vẽ BH vuông góc với CM, nối DH, vẽ HN vuông góc với DH (N BC) - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 42: Cho hình vuông ABCD, trên AB lấy điểm M, vẽ BH vuông góc với CM, nối DH, vẽ HN vuông góc với DH (N BC) (Trang 23)

Bài 49: Cho M, N lần lượt là trung điểm các cạnh AD và BC của hình chữ nhật, E là điểm trên tia DC, K là giao EM và AC, CMR: MN là tia phân giác ·KNE - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 49: Cho M, N lần lượt là trung điểm các cạnh AD và BC của hình chữ nhật, E là điểm trên tia DC, K là giao EM và AC, CMR: MN là tia phân giác ·KNE (Trang 27)

Bài 5 4: Cho hình thang ABCD, đáy lớn CD vàO là giao điểm của hai đường chéo, đường thẳng qu aB và //AD cắt AC tại E, đường thẳng qua C //AD cắt BD tại F, CMR : - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 5 4: Cho hình thang ABCD, đáy lớn CD vàO là giao điểm của hai đường chéo, đường thẳng qu aB và //AD cắt AC tại E, đường thẳng qua C //AD cắt BD tại F, CMR : (Trang 29)

a, CMR: Tứ giác BCED là hình thang - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — a CMR: Tứ giác BCED là hình thang (Trang 32)

Vậy BCED là hình thang - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — y BCED là hình thang (Trang 32)

a, Tứ giác MNPC là hình gì? b, CMR : MNND - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — a Tứ giác MNPC là hình gì? b, CMR : MNND (Trang 33)

Bài 6 1: Cho hình vuông ABCD có cạnh a, Gọi I là trung điểm AB, Trên tia đối của tia CD đặt điểm M sao cho CM=a, Trên tia đối của tia CB đặt điểm N sao cho CN =2a, trên tia đối của tia DC đặt điểm P sao cho DP =2a, trên tia đối của tia AD đặt Q sao cho A - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 6 1: Cho hình vuông ABCD có cạnh a, Gọi I là trung điểm AB, Trên tia đối của tia CD đặt điểm M sao cho CM=a, Trên tia đối của tia CB đặt điểm N sao cho CN =2a, trên tia đối của tia DC đặt điểm P sao cho DP =2a, trên tia đối của tia AD đặt Q sao cho A (Trang 34)

d, ABCD là hình vuông thì  NMD là vuông cân tạ iN e, Diện tích ABCD bằng 4cm 2 - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — d ABCD là hình vuông thì  NMD là vuông cân tạ iN e, Diện tích ABCD bằng 4cm 2 (Trang 34)

Bài 6 5: Cho hình thang ABCD (AB//CD), Có AB=a, CD= b, M, N trên các cạnh AD và BC sao cho MN//CD và - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 6 5: Cho hình thang ABCD (AB//CD), Có AB=a, CD= b, M, N trên các cạnh AD và BC sao cho MN//CD và (Trang 35)

=> ADFE là hình thang có MN là đường trung bình => - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — gt ; ADFE là hình thang có MN là đường trung bình => (Trang 35)

Bài 6 8: Cho hình thoi ABCD có µA  600 ,P là 1 điểm thuộc cạnh AB, N là giao điểm của hai đường thẳng AD và CP - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 6 8: Cho hình thoi ABCD có µA  600 ,P là 1 điểm thuộc cạnh AB, N là giao điểm của hai đường thẳng AD và CP (Trang 36)

Bài 75: Cho hình thang (AD//BC). Một điểm M di động trên đường chéo AC, Chứng minh: - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 75: Cho hình thang (AD//BC). Một điểm M di động trên đường chéo AC, Chứng minh: (Trang 39)

ADE ADB ADF ADC AEF ACB - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — ADE ADB ADF ADC AEF ACB (Trang 39)

b) Gọi H, I, K là hình chiếu củ aM trên AB, DE, AC, Chứng minh DH=DI, EI=EK - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — b Gọi H, I, K là hình chiếu củ aM trên AB, DE, AC, Chứng minh DH=DI, EI=EK (Trang 40)

Bài 79: Cho hình bình hành ABCD có đường chéo AC lớn hơn đường chéo BD, Gọi E,F lần lượt là hình chiếu của B và D xuống đường thẳng AC, Gọi H và K lần lượt là hình chiếu của C xuống AB và AD - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 79: Cho hình bình hành ABCD có đường chéo AC lớn hơn đường chéo BD, Gọi E,F lần lượt là hình chiếu của B và D xuống đường thẳng AC, Gọi H và K lần lượt là hình chiếu của C xuống AB và AD (Trang 41)

Bài 82: Cho hình thoi ABCD, Có BAD · 1200, Gọi M là 1 điểm nằm trên cạnh AB, Hia đường thẳng - Chuyên Đề Tam Giác Đồng Dạng Bồi Dưỡng HSG Toán 8 Có Lời Giải Chi Tiết — i 82: Cho hình thoi ABCD, Có BAD · 1200, Gọi M là 1 điểm nằm trên cạnh AB, Hia đường thẳng (Trang 42)

TỪ KHÓA LIÊN QUAN

TÀI LIỆU CÙNG NGƯỜI DÙNG

TÀI LIỆU LIÊN QUAN