Nghiên cứu biến dạng đàn hồi của hợp kim thay thế AB xen kẽ c sử dụng phương pháp thống kê mômen
MỤC LỤC
Mục đích nghiên cứu
Nghiên cứu biến dạng đàn hồi của HKTT AB xen kẽ nguyên tử C với cấu trúc LPTD ở áp suất không khi tính đến ảnh hưởng phi điều hòa của dao động mạng được xây dựng trên PPTKMM trong đó đưa ra biểu thức giải tích của năng lượng tự do, khoảng cách trung bình giữa các nguyên tử, các môđun đàn hồi E, G, K và các hằng số đàn hồi C11, C12, C44 phụ thuộc vào nhiệt độ và nồng độ nguyên tử thay thế và nồng độ nguyên tử xen kẽ. Khi nồng độ nguyên tử thay thế B bằng không thì kết quả tính toán đối với HKTT AB xen kẽ nguyên tử C là kết quả tính toán đối với HKXK AC và kết quả tính toán đối với HKTT AB là kết quả tính toán đối với kim loại chính A.
Phương pháp nghiên cứu
Về nguyên tắc, có thể áp dụng PPTKMM để nghiên cứu các tính chất cấu trúc, nhiệt động, đàn hồi, khuếch tán, chuyển pha, … của các loại tinh thể khác nhau như kim loại, hợp kim, tinh thể và hợp chất bán dẫn, chất bán dẫn có kích thước nano, tinh thể ion, tinh thể phân tử, tinh thể khí trơ, siêu mạng, tinh thể lượng tử, màng mỏng, graphen,… với các cấu trúc LPTK, LPTD, LGXC, kim cương, sunfua kẽm, florite,… trong khoảng rộng của nhiệt độ từ 0 K đến nhiệt độ nóng chảy và dưới tỏc dụng của ỏp suất. Có thể kết hợp PPTKMM với các phương pháp khác như phương pháp biến phân 4ung, phương pháp từ các nguyên lý đầu tiên, mô hình tương quan phi điều hòa của Einstein, phương pháp phonon tự hợp, phương pháp hàm phân bố một hạt, phương pháp trường tự hợp, … Một nhóm các nhà nghiên cứu ở Việt Nam, Nhật Bản và Hàn Quốc đang phát triển mạnh PPTKMM trong thời gian gần đây.
Bố cục của luận văn
Hợp kim và hợp kim xen kẽ
Đối với hợp kim xen kẽ (hoặc hợp kim ngoài nút), các nguyên tử kim loại ở nút mạng tinh thể được giữ nguyên và xen kẽ vào các chỗ trống là các nguyên tử khác có kích thước bé hơn như silic, liti, hiđrô,…với nồng độ hạt xen kẽ rất nhỏ cỡ vài phần trăm. Một sự hiểu biết đầy đủ hơn về cấu trúc của các kim loại, các pha nhị nguyên và tam nguyên của các kim loại và phi kim loại chứng tỏ rằng nói chung ở nồng độ thấp của nguyên tử nhỏ, có thể mô tả pha như một dung dịch và điều này gần đúng với mô tả lịch sử của hợp chất xen kẽ nói trên.

Các phương pháp lý thuyết chủ yếu trong nghiên cứu biến dạng đàn hồi của kim loại và hợp kim
Trong quá trình áp dụng, phương pháp TB tỏ ra là một phương pháp có nhiều ưu điểm như cung cấp thông tin về cấu trúc điện tử của vật liệu mô hình và có hiệu quả tính toán cao hơn nhiều so với các phương pháp abinitio.Tuy nhiên phương pháp TB có nhược điểm ở chỗ nó phụ thuộc vào việc làm khớp với số liệu thực nghiệm hoặc các số liệu tính toán từ phương pháp ab-initio.Số hạng năng lượng đẩy chỉ có thể xác định bằng một công thức kinh nghiệm.Phương pháp đòi hỏi giải ít nhất một bài toán trị riêng hoặc vectơ riêng của ma trận bằng mô phỏng MD. Trong những năm gần đây, một phương pháp là phương pháp phần tử hữu hạn FEM (Finite Element Method) được phát triển mạnh và sử dụng rộng rãi trong nghiên cứu tính chất cơ của kim loại, hợp kim nói chung và nghiên cứu về các quá trình đàn- dẻo cũng như đàn hồi của các vật liệu nói riêng [30,31].Phương pháp này được áp dụng trong cả hai quá trình rắn –dẻo và đàn-dẻo [31].
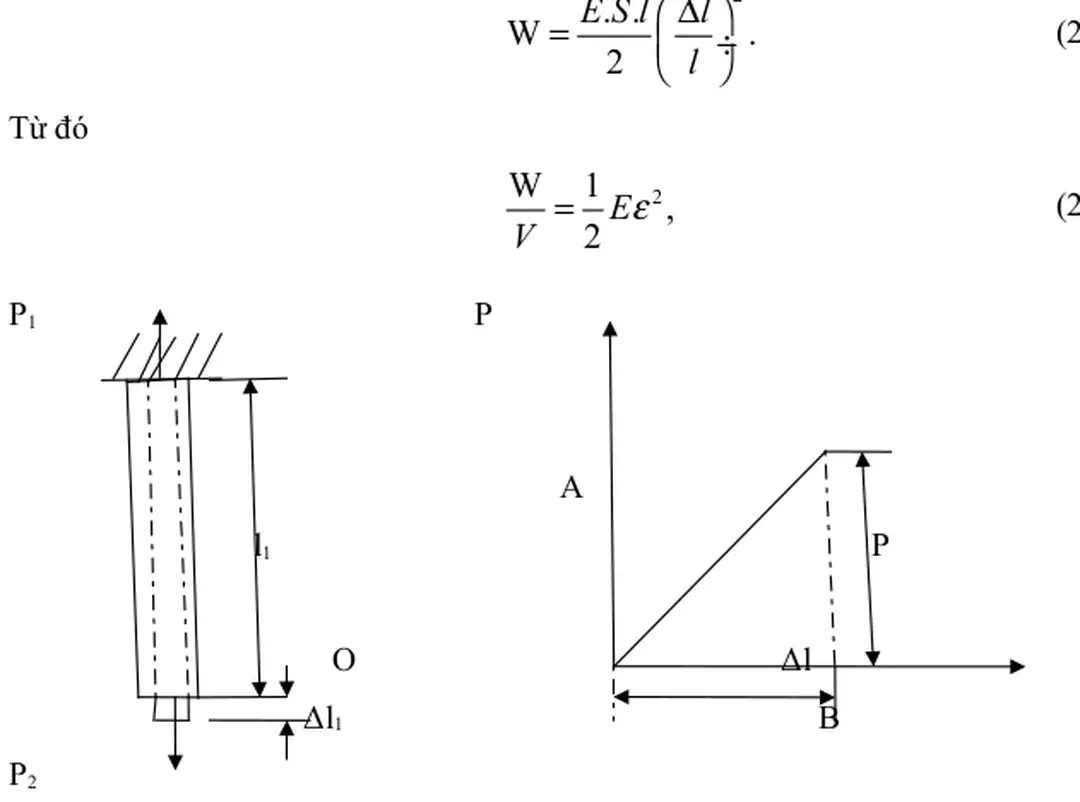
Lý thuyết biến dạng
Phương pháp thống kê mômen (PPTKMM) đã được nhiều tác giả sử dụng rộng rãi để nghiên cứu biến dạng đàn hồi của nhiều loại tinh thể khác nhau như kim loại, hợp kim, tinh thể và hợp chất bán dẫn, oxit, màng mỏng, siêu mạng, tinh thể khí trơ,…với các cấu trúc LPTK, LPTD, LGXC, lập phương kiểu kim cương, sunfua kẽm ở áp suất không và dưới tác dụng của áp suất [2-10]. Trong biến dạng phi tuyến,khi các nguyên tử dịch chuyển sang vị trí mới, để không gây nên sự phá hủy các mối liên kết, ta phải đảm bảo điều kiện là khoảng cách giữa các nguyên tử không được vượt quá kích thước vùng lực tác dụng tương hỗ kéo giữa các nguyên tử trong suốt quá trình nguyên tử dịch chuyển.

Phương pháp thống kê mômen[7]
Khi đạo hàm theo ngoại lực ak đối với điều kiện chuẩn hóa của toán tử thống kê (Trρ =ˆ 1 ) và sử dụng các công thức toán tử do Kirznitz đưa ra trong [60]. Hàm tương quan giữa đại lượng F (được đặc trưng bởi toán tử Fˆ ) và tọa độ suy rộngQˆk đối với hệ ứng với Hamilton Hˆ được xác định bởi hàm ˆ , ˆk ,. là ký hiệu phản giao hoán tử và hàm này được cho bởi. trong đó B2nlà hệ số Bernoulli. Nhờ Hˆ0 ta có thể xác đinh được thăng giáng của xung lượng. và hàm tương quan giữa Fˆ và Qˆk đối với hệ ứng với HamiltonienHˆ0. .14) Công thức trên cho phép xác định sự tương quan giữa các đại lượng F và tọa độ suy rộng Qk.
Nghiên cứu biến dạng đàn hồi của kim loại với cấu trúc LPTD ở áp suất P= 0[7]
Trong chương 2, chúng tôi trình bày nội dung của PPTKMM trong đó đề cập đến định nghĩa của các mômen và hàm tương quan, các công thức tổng quát về mômen, áp dụng công thức mômen để tính năng lượng tự do của hệ lượng tử và áp dụng PPTKMM để rút ra biểu thức giải tích của khoảng lân cận gần nhất, năng lượng tự do, các môđun đàn hồi và các hằng số đàn hồi của kim loại với cấu trúc LPTD ở áp suất không. Bằng PPTKMM và dựa trên nghiên cứu biến dạng đàn hồi của hợp kim thay thế hai thành phần với cấu trúc LPTD, chúng tôi rút ra biểu thức giải tích đối với khoảng lân cận gần nhất trung bình, năng lượng tự do và các đại lượng đặc trưng cho biến dạng đàn hồi như các môđun đàn hồi và các hằng số đàn hồi của hợp kim xen kẽ hai thành phần và hợp kim thay thế hai thành phần xen kẽ thành phần thứ ba với cấu trúc LPTD.
Thế tương tác giữa các nguyên tử trong hợp kim xen kẽ
Đối với tinh thể kim loại và khí trơ có cấu trúc lập phương, ở trạng thái lí tưởng mỗi nút mạng được chiếm giữ bởi một nguyên tử và coi rằng giữa 2 nguyên tử bất kỳ nằm gần nhau không xảy ra tương tác hóa học ở điều kiện thường. (3.7) với là khoảng cách giữa hai nguyên tử tương ứng thế năng cực tiểu lấy giá trị - D, m, n là các số có giá trị khác nhau đối với các nguyên tử kim loại khác nhau và được xác định bằng kinh nghiệm dựa trên cơ sở các số liệu thực nghiệm.

Các thông số của kim loại và hợp kim xen kẽ 1. Các thông số của kim loại
Để áp dụng tính số đối với các đại lượng đàn hồi của hợp kim thay thế AB xen kẽ nguyên tử Cvới cấu trúc LPTD theo các biểu thức giải tích thu được ở trên, ta làm như sau. Xác định khoảng lân cận gần nhất giữa hai hạt (0, 0) trong HKXK AC ở nhiệt độ 0K (0, 0) từ phương trình trạng thái hoặc điều kiện cực tiểu của năng lượng liên kết.
Biến dạng đàn hồi của các hợp kim thay thế hai thành phần với cấu trúc LPTD ở áp suất P = 0
Các kết quả tính toán đối với sự phụ thuộc nhiệt độ và nồng độ nguyên tử thay thế của các môđun đàn hồi của một số hợp kim thay thế hai thành phần ở P = 0 được tổng kết trong các bảng số từ Bảng 3.8 đến Bảng 3.13 và được minh họa trên các hình vẽ từ Hình 3.6 đến Hình 3.11. Các kết quả tính toán đối với sự phụ thuộc nhiệt độ và nồng độ nguyên tử thay thế của các hằng số đàn hồi của một số hợp kim thay thế hai thành phần ở áp suất không được tổng kết trong các bảng số từ Bảng 3.14 đến Bảng 3.18 và được minh họa trên các hình vẽ từ Hình 3.12 đến Hình 3.18.

Biến dạng đàn hồi của các hợp kim xen kẽ hai thành phần AuLi với cấu trúc LPTD ở áp suất P = 0
Ở nồng độ nguyên tử xen kẽ bằng không, ta thu được khoảng lân cận gần nhất của kim loai sạch Au trong [3]. Khi nồng độ nguyên tử xen kẽ Li bằng không, ta thu được các môđun đàn hồi E, G, K của kim loại Au trong [3].

Biến dạng đàn hồi của các hợp kim xen kẽba thành phần AuCuLi với cấu
Áp dụng các kết quả lý thuyết ở chương 2 khi sử dụng thế n-m và phương pháp ba quả cầu phối vị, chúng tối thực hiện tính số cho các đại lượng đặc trưng cho biến dạng đàn hồi như khoảng lân cận gần nhất trung bình, các môđun đàn hồi E, G, K và các hằng số đàn hồi C11, C12, C44 đối với một số hợp kim thay thế hai thành phần, hợp kim xen kẽ hai thành phần và hợp kim xen kẽ ba thành phần (hợp kim thay thế hai thành phần xen kẽ thành phần thứ ba) và xác định sự phụ thuộc nhiệt độ, nồng độ nguyên tử thay thế và nồng độ nguyên tử xen kẽ của các đại lượng này đối với các hợp kim ở áp suất không. Chúng tôi tìm được qui luật về sự phụ thuộc nhiệt độ, nồng độ nguyên tử thay thế và nồng độ nguyên tử xen kẽ của khoảng lân cận gần nhất trung bình, các môđun đàn hồi E, G, K và các hằng số đàn hồi C11, C12, C44 đối với các hợp kim nghiên cứu và qui luật này hoàn toàn phù hợp với thực nghiệm.Các kết quả tính toán đối với kim loại ởáp suất không được so sánh với số liệu thực nghiệmvà nhiều kết quả tính toán có sự phù hợp rất tốt.
