Một số kiến thức về vành và trường
1.1.1 Định nghĩa vành Vành là một tập hợp cùng với hai phép toán hai ngôi đã cho trong kí hiệu theo thứ tự bằng các dấu và (người ta thường kí hiệu như vậy) và gọi là phép cộng và phép nhân sao cho các điều kiện sau thỏa mãn:
1) cùng với phép cộng là một nhóm aben
2) cùng với phép nhân là một nửa nhóm
3) Phép nhân phân phối đối với phép cộng: với các phần tử tùy ý ta có
Trong phép cộng, phần tử trung lập được ký hiệu là 0 và được gọi là phần tử không Đối với mỗi phần tử trong phép cộng, phần tử đối xứng được ký hiệu là -a và được gọi là đối của a.
Nếu phép nhân có tính giao hoán, nghĩa là , thì vành đƣợc gọi là vành giao hoán
Trong toán học, nếu phép nhân có phần tử trung lập, phần tử này được gọi là phần tử đơn vị và thường được ký hiệu là 1 Vành mà trong đó phép nhân có phần tử đơn vị được gọi là vành có đơn vị.
Cho vành có đơn vị Xét tập hợp
Ta nói vành đƣợc gọi là vành địa phương nếu tập hợp là một nhóm con của đối với phép cộng
Vành giao hoán hữu hạn được gọi là vành chuỗi nếu tất cả các iđêan của nó tạo thành một chuỗi sắp thứ tự tuyến tính theo quan hệ bao hàm.
Ví dụ Vành với là số nguyên tố là vành chuỗi giao hoán hữu hạn
1.1.2 Ƣớc của không Miền nguyên
1.1.2.1 Định nghĩa Giả sử là một vành giao hoán Ta bảo một phần tử là bội của một phần tử hay chia hết cho , kí hiệu , nếu có sao cho ; ta còn nói rằng là ước của hay chia hết , kí hiệu |
1.1.2.2 Định nghĩa Ta gọi là ước của 0 mọi phần tử sao cho có thỏa mãn quan hệ a
1.1.2.3 Định nghĩa Ta gọi là miền nguyên một vành có nhiều hơn một phần tử, giao hoán, có đơn vị, không có ƣớc của 0
Ví dụ Vành số nguyên là một miền nguyên
1.1.3.1 Mệnh đề Một bộ phận khác rỗng của một vành là một iđêan của nếu và chỉ nếu các điều kiện sau thỏa mãn:
(ii) và với mọi và mọi
Một vành giao hoán có đơn vị khác không được gọi là tối đại nếu các iđêan của nó chỉ chứa bản thân và không Nguyên tố được xác định khi iđêan chỉ chứa phần tử và tích của nó Ngoài ra, iđêan chính là iđêan được sinh bởi một phần tử.
1.1.3.2 Mệnh đề ([12]) Cho là vành giao hoán hữu hạn Khi đó, các phát biểu sau đây là tương đương:
(i) là vành địa phương và iđêan tối đại của là iđêan chính;
(ii) là vành iđêan chính, địa phương;
1.1.3.3 Định lý Giả sử là một vành giao hoán có đơn vị và Bộ phận của gồm các phần tử có dạng với là iđêan của sinh ra bởi
1.1.3.4 Mệnh đề Nếu là một vành có đơn vị và nếu là một iđêan của chứa đơn vị của thì ta có
1.1.3.5 Mệnh đề Nếu là một iđêan của vành , thì:
(i) Lớp chỉ phụ thuộc vào các lớp và mà không phụ thuộc vào sự lựa chọn của các phần tử từ các lớp đó
(ii) ⁄ cùng với hai phép toán
là một vành gọi là vành thương của trên A
1.1.4 Định nghĩa đồng cấu vành Một đồng cấu (vành) là một ánh xạ từ một vành đến một vành sao cho
Với mọi Nếu thì đồng cấu gọi là một tự đồng cấu của
1.1.5 Định nghĩa trường Ta gọi là trường một miền nguyên trong đó mọi phần tử khác không đều có một nghịch đảo trong vị nhóm nhân Vậy một vành giao hoán, có đơn vị, có nhiều hơn một phần tử là một trường nếu và chỉ nếu { } là một nhóm đối với phép nhân của
Tập hợp các số hữu tỉ, kết hợp với phép cộng và phép nhân, tạo thành một trường Ngoài ra, chúng ta còn có các trường số thực và số phức.
1.1.6.1 Định nghĩa Cho là một vành có đơn vị khác không Một là:
(ii) Ánh xạ đƣợc gọi là phép nhân môđun, thỏa các điều kiện sau:
3 Quy tắc unita: trong đó là các phần tử tùy ý của
Lúc đó, đƣợc gọi là vành cơ sở Nếu là một ta ký hiệu Tương tự ta cũng định nghĩa được khái niệm
Nhận xét Từ định nghĩa ta có kết quả sau: với mọi
1.1.6.2 Định nghĩa Một trái là đơn nếu nó không có một môđun con không tầm thường nào
Một trái là nửa đơn trái nếu là một tổng trực tiếp của các môđun đơn
Một vành là nửa đơn trái nếu là một tổng trực tiếp các iđêan trái cực tiểu
1.1.7 Môđun con và môđun thương
1.1.7.1 Định nghĩa (Môđun con) Cho là một phải Tập con của đƣợc gọi là môđun con của , ký hiệu hay , nếu là một phải với phép toán cộng và nhân môđun hạn chế trên
Khi phân biệt các ký hiệu, cần lưu ý rằng ký hiệu này khác với ký hiệu tập hợp thông thường Cụ thể, ký hiệu biểu thị môđun con của , trong khi ký hiệu chỉ ra rằng không phải là môđun con của
Sau đây là dấu hiệu nhận biết một môđun con:
1.1.7.2 Định lý Giả sử là một phải Nếu là một tập con khác của , thì các khẳng định sau là tương đương:
(ii) là nhóm con của nhóm cộng của môđun và với mọi ta có ,
(iii) Với mọi ta có , và với mọi ta có
Vành giao hoán được xác định bởi số nguyên dương nhỏ nhất, gọi là đặc số, mà với mọi phần tử trong vành Nếu không tồn tại số nguyên dương như vậy, vành được coi là có đặc số 0 Phần tử trong vành được gọi là phần tử lũy linh nếu tồn tại một số nguyên sao cho phần tử đó có thể biểu diễn dưới dạng lũy thừa Chỉ số lũy linh của phần tử a là số tự nhiên nhỏ nhất thỏa mãn tính chất này.
Các khái niệm sau là quen thuộc đối với vành chuỗi giao hoán hữu hạn [21]
Hai đa thức [ ] đƣợc gọi là nguyên tố cùng nhau nếu 〈 〉 〈 〉 [ ], hoặc tương đương, nếu tồn tại các đa thức [ ] sao cho
Nguyên tố cùng nhau của hai đa thức trong vành được định nghĩa tương tự như trong các trường hợp khác Nếu vành là vành chuỗi giao hoán hữu hạn, thì nó trở thành một trường, trong đó là iđêan tối đại của vành chuỗi giao hoán hữu hạn Hai đa thức trong vành được coi là nguyên tố cùng nhau khi và chỉ khi chúng không có ước chung nào có bậc lớn hơn 0.
Các kết quả sau chỉ ra mối liên hệ giữa các phần tử của vành [ ] và [ ]
1.1.8 Bổ đề ([21]) Với bất kỳ vành chuỗi giao hoán hữu hạn , hai đa thức [ ] là nguyên tố cùng nhau khi và chỉ khi và là nguyên tố cùng nhau trong vành [ ]
1.1.9 Nhận xét ([21]) Cho là vành chuỗi giao hoán hữu hạn Giả sử rằng là các đa thức đôi một nguyên tố cùng nhau trong vành [ ] Khi đó, và
∏ nguyên tố cùng nhau trong vành [ ]
Một đa thức được xem là bất khả quy cơ sở khi nó không thể phân tích trong vành Đồng thời, một đa thức được gọi là chính quy nếu nó không phải là ước của một đa thức khác.
1.1.10 Bổ đề ([21, theorem XIII.4]) (Bổ đề Hensel) Cho là một đa thức trên vành
Giả sử với đôi một nguyên tố cùng nhau trên vành
Khi đó, tồn tại các đa thức đôi một nguyên tố cùng nhau sao cho và với
1.1.11 Định nghĩa ([27]) Cho vành giao hoán hữu hạn và đa thức
[ ] (i) Ta gọi là đa thức đơn biến nếu
Một đa thức được gọi là hoàn toàn không chính phương nếu trong phân tích thành phần của nó, không có nhân tử nào được lặp lại, tức là tất cả các nhân tử đều là các đa thức bất khả quy khác nhau.
Một số kiến thức về mã tuyến tính
Trường hữu hạn đóng vai trò quan trọng trong lý thuyết mã, được phát triển từ định lý của Shannon năm 1948 Để nâng cao các mã constacyclic, các nhà toán học đã mở rộng nghiên cứu về cấu trúc mã trên vành hữu hạn, từ đó tạo ra sự đa dạng trong lựa chọn bảng chữ cái khi xem xét mã.
Mục này nhằm trình bày các kiến thức cơ sở của mã tuyến tính trên vành giao hoán hữu hạn
1.2.1 Định nghĩa Cho là vành giao hoán hữu hạn và
(i) Tập con của vành đƣợc gọi là một mã có độ dài trên vành
Tập con của vành được định nghĩa là một mã tuyến tính có độ dài trên vành nếu nó là môđun con của môđun Mỗi phần tử trong tập con này được gọi là một từ mã của mã.
1.2.2 Định nghĩa Cho vành giao hoán hữu hạn và mã tuyến tính có độ dài trên Tích trong (hay tích chấm) của hai từ mã và của đƣợc định nghĩa nhƣ sau:
1.2.3 Định nghĩa Hai từ mã đƣợc gọi là trực giao nếu Với mỗi mã tuyến tính trên vành , mã đối ngẫu là tập hợp các phần tử của vành trực giao với tất cả phần tử của , tức là { | }
Một mã đƣợc gọi là tự trực giao nếu Mã đƣợc gọi là tự đối ngẫu nếu
Trong quá trình truyền tải thông tin, "tiếng ồn" là yếu tố gây nhiễu không thể tránh khỏi, dẫn đến sự sai khác giữa mã ban đầu và mã nhận được Để xác định chính xác mã di truyền ban đầu, các nhà khoa học đã đưa ra một số định nghĩa như khoảng cách Hamming, khoảnh cách thuần nhất, khoảng cách Lee và khoảng cách Euclid Trong bài viết này, chúng ta sẽ nhắc lại khái niệm trọng Hamming (Hamming weight) và khoảng cách Hamming (Hamming distance).
1.2.4 Định nghĩa Cho là một vành giao hoán hữu hạn và là một mã có độ dài trên vành Khi đó:
(i) Trọng Hamming (Hamming weight) của từ mã , ký hiệu là là số các thành phần khác 0 của
(ii) Khoảng cách Hamming (Hamming distance) của hai từ mã là số thành phần khác nhau giữa chúng hay chính là
Trong mã tuyến tính, trọng Hamming và khoảng cách Hamming là hai khái niệm tương đương, được xác định là trọng Hamming nhỏ nhất của các từ mã khác 0.
1.2.5 Định lý ([10]) Cho là một mã cyclic có độ dài trên trường Khi đó, mã có dạng 〈 〉 〈 [ ]
Năm 2009, D Q Hai đã mô tả mã cyclic có độ dài trên vành nhƣ sau:
〉 là vành địa phương với iđêan tối đại là
〈 〉 nhưng ( 〈 〉 )[ ] không phải là vành chuỗi
(ii) Mã cyclic có độ dài trên vành chính là iđêan của vành
- Loại 2: Iđêan chính có phần tử sinh là đa thức không phải là đa thức đơn biến
- Loại 3: Iđêan chính có phần tử sinh là đa thức đơn biến
Với và hoặc khả nghịch có thể biểu diễn dưới dạng ∑ , với
〉 với và với là số nguyên nhỏ nhất sao cho
〈 〉 với tương tự trong mã loại 3 và
(iii) Số các mã cyclic có độ dài trên vành là
(iv) Giả sử là mã cyclic có độ dài trên vành Khi đó, số từ mã của được tính bởi công thức sau:
- Nếu 〈 〉 với , và khả nghịch thì
- Nếu 〈 〉 với , , hoặc khả nghịch và
Mã constacyclic và mã đối ngẫu của chúng
Cho là một trường hữu hạn, dãy gồm số hạng , phép chuyển cyclic τ và phép chuyển negacyclic ν trên đƣợc định nghĩa nhƣ sau: và
Mã được gọi là cyclic khi nó thỏa mãn điều kiện nhất định, trong khi mã negacyclic cũng có những tiêu chí riêng Cụ thể, nếu λ là một phần tử khả nghịch, thì phép chuyển đổi trên mã được xác định, và mã sẽ được gọi là cyclic nếu nó đóng với phép chuyển này Theo định nghĩa, khi mã thỏa mãn điều kiện nhất định, nó sẽ được phân loại là mã cyclic hoặc negacyclic.
Mỗi từ mã có thể được coi như một đa thức biểu diễn, và mã được xác định bởi tập hợp tất cả các đa thức biểu diễn các từ mã của nó Trong vành thương, các đa thức này đóng vai trò quan trọng trong việc xác định cấu trúc của mã.
〈 〉, tương ứng là ảnh của qua phép chuyển Từ đó, các mệnh đề sau đây đƣợc biết đến và là hiển nhiên ([15], [22])
2.1.1 Mệnh đề Mã tuyến tính có độ dài là mã trên khi và chỉ khi là một iđêan của vành thương 〈 [ ]
〉 là vành iđêan chính, những iđêan được tạo bởi
Mã đối ngẫu của mã cyclic là mã cyclic, trong khi mã đối ngẫu của mã negacyclic là mã negacyclic Điều này dẫn đến một mệnh đề kéo theo quan trọng về mã đối ngẫu trong lĩnh vực mã hóa.
2.1.2 Mệnh đề Mã đối ngẫu của mã là mã
Cho là một mã có độ dài trên Xét phần tử bất kỳ , và Vì là , Do đó
Có nghĩa là Vì vậy, đóng đối với phép chuyển , có nghĩa là là một mã
2.1.3 Mệnh đề Cho là phần tử khác 0, thuộc và
Khi đó, trong vành 〈 [ ] 〉 khi và chỉ khi trực giao với và tất cả phép chuyển
Cho biểu thị phép chuyển của cho những từ mã có độ dài , nghĩa là cho mỗi ,
Cho là số nguyên dương nhỏ nhất mà Với ,
Do đó, là tất cả phép chuyển của
Do đó khi và chỉ khi khi và chỉ khi với khi và chỉ khi trực giao với và tất cả phép chuyển Điều phải chứng minh
2.1.4 Định nghĩa Cho vành , là tập con khác rỗng của , linh tử hóa của , ký hiệu là là tập hợp
{ | } Nếu S là một iđêan của thì cũng là một iđêan của
Thông thường, với một đa thức bậc , đa thức đảo của nó sẽ được ký hiệu bằng Vì vậy, nếu thì )
Lưu ý rằng hệ số tự do chỉ khác 0 trong một số trường hợp nhất định, điều này tương đương với một điều kiện cụ thể Theo định nghĩa, chúng ta dễ dàng nhận thấy rằng nếu { | } được ký hiệu, thì nếu là một iđêan, nó cũng sẽ là một iđêan khác.
2.1.5 Mệnh đề Cho hoặc Giả sử là một mã có độ dài trên Khi đó mã đối ngẫu của là
Chứng minh Ở đây Theo Mệnh đề 2.1.2, ta có đƣợc dữ kiện là mã có độ dài trên Do đó, theo Mệnh đề 2.1.1, cả và là iđêan của vành 〈 [ ]
〉 Khẳng định này xuất phát từ Mệnh đề 2.1.3
2.2 Tất cả mã constacyclic có độ dài
Cho và là hai phần tử khác của ; , ; với , và Trước tiên chúng ta xem xét mã có độ dài trên
2.2.1 Bổ đề Tồn tại , sao cho và
Bằng các thuật toán chia, tồn tại số nguyên không âm , mà và
Giả sử và Vì , là các phần tử khác không của , , và Vì vậy, ta có
2.2.2 Mệnh đề Cho và được định nghĩa
Khi đó và là đẳng cấu vành
Với đa thức [ ], khi và chỉ khi có [ ] sao cho , tương đương với
Điều này có nghĩa là mọi yếu tố đều được xác định rõ ràng và tương ứng một cách chính xác Rõ ràng, cấu trúc này là một đồng cấu vành, do đó, nó được xem là một đẳng cấu vành Bằng cách chứng minh tương tự, chúng ta cũng có thể khẳng định rằng yếu tố kia cũng là một đẳng cấu vành.
2.2.3 Hệ quả Cho 〈 [ ] 〉 〈 [ ] 〉 Khi đó A là mã negacyclic có độ dài trên khi và chỉ khi là mã có độ dài trên , và
B là mã cyclic có độ dài trên khi và chỉ khi là mã có độ dài trên
Sử dụng đẳng cấu, chúng tôi đã đạt được kết quả bao gồm mã negacyclic và mã cyclic, được trình bày chi tiết trong các phần 3 và 4 [13], cho phép chuyển đổi tương ứng giữa các loại mã này.
2.2.4 Định lý Giả sử p là một số nguyên tố lẻ, , Θ là các phần tử của sao cho với là các phần tử khác không thuộc Cho được định nghĩa như trong Bổ đề 2.2.1
(i) Giả sử (m bất kỳ), hoặc (m chẵn), cố định một phần tử γ sao cho , mã có độ dài trên là
Mỗi mã 〈 〉 chứa từ mã
(ii) Giả sử (m lẻ), mã có độ dài trên là 〈 〉 〈 [ ] 〉 Mỗi mã 〈 〉 chứa từ mã
(iii) Mã Θ-constacyclic có độ dài trên là
Mỗi mã 〈 〉 chứa từ mã
Theo như phần 3 [13] cho ξ là nghiệm của phương trình sao cho { }
Rõ ràng, các mã có độ dài khác nhau là rời nhau Chúng tôi sẽ tập trung nghiên cứu tất cả mã có độ dài trên Nếu điều kiện được thỏa mãn, cấu trúc của mã sẽ được trình bày theo Định lý 2.2.4 (iii) Dưới đây là một vài kết quả liên quan đến nghiên cứu của chúng tôi.
(i) và m lẻ, tồn tại sao cho
(ii) (m chẵn), tồn tại Hơn nữa, bất khả quy trong [ ]
Khi đó không tồn tại sao cho , mà,
Nhƣ vậy, (i) đƣợc chứng minh
Bây giờ giả sử ( chẵn) Bằng thuật toán chia, tồn tại các số nguyên không âm sao cho
Tức là, Vì ( chẵn) Tồn tại sao cho Nhƣ vậy, bằng cách xây dựng nhƣ trên,
Giả sử khả quy trong , tồn tại ν mà Do đó, Điều này mâu thuẫn
Vậy, là bất khả quy trên
2.2.6 Định lý Giả sử hoặc , m chẵn Cho được xác định duy nhất trong Bổ đề 2.2.5 có độ dài trên
Mỗi mã 〈 〉 chứa từ mã
Theo Bổ đề 2.2.5.(ii), là bất khả quy trên [x] Vì vậy, hệ số thành sản phẩm của hệ số bất khả quy trong nhƣ là
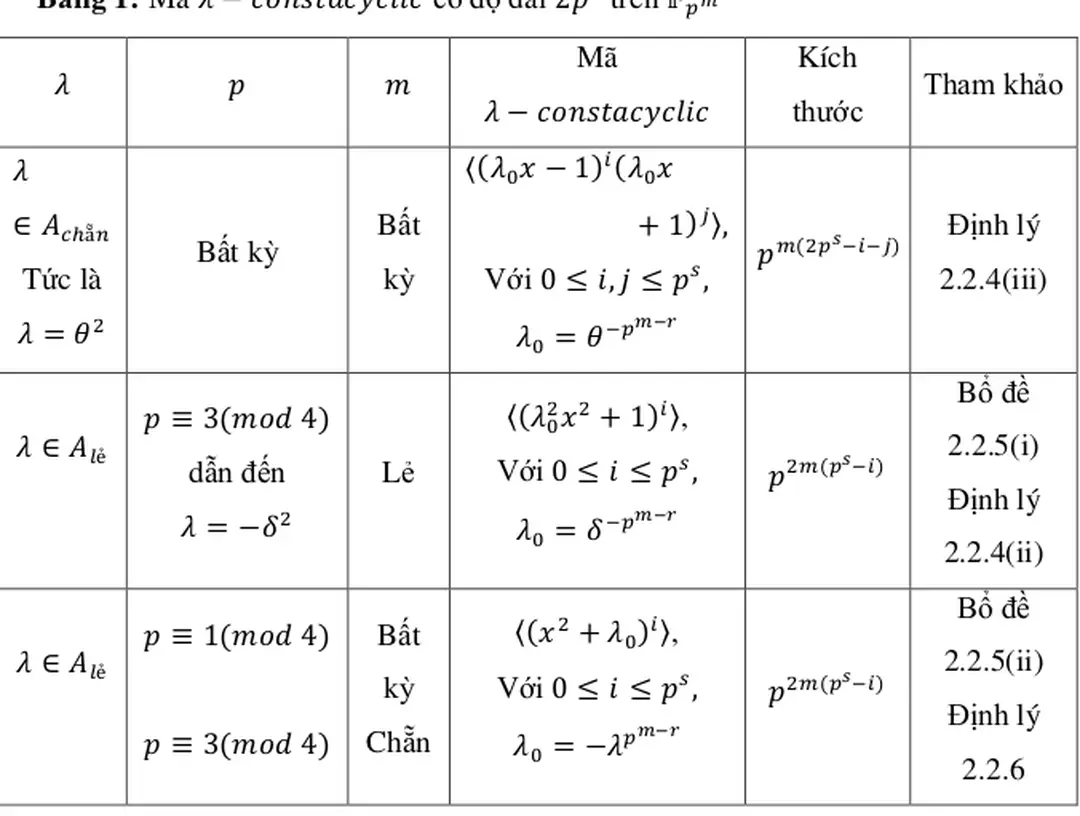
Bảng 1: Mã có độ dài trên
Bổ đề 2.2.5(i) Định lý 2.2.4(ii)
Bổ đề 2.2.5(ii) Định lý 2.2.6
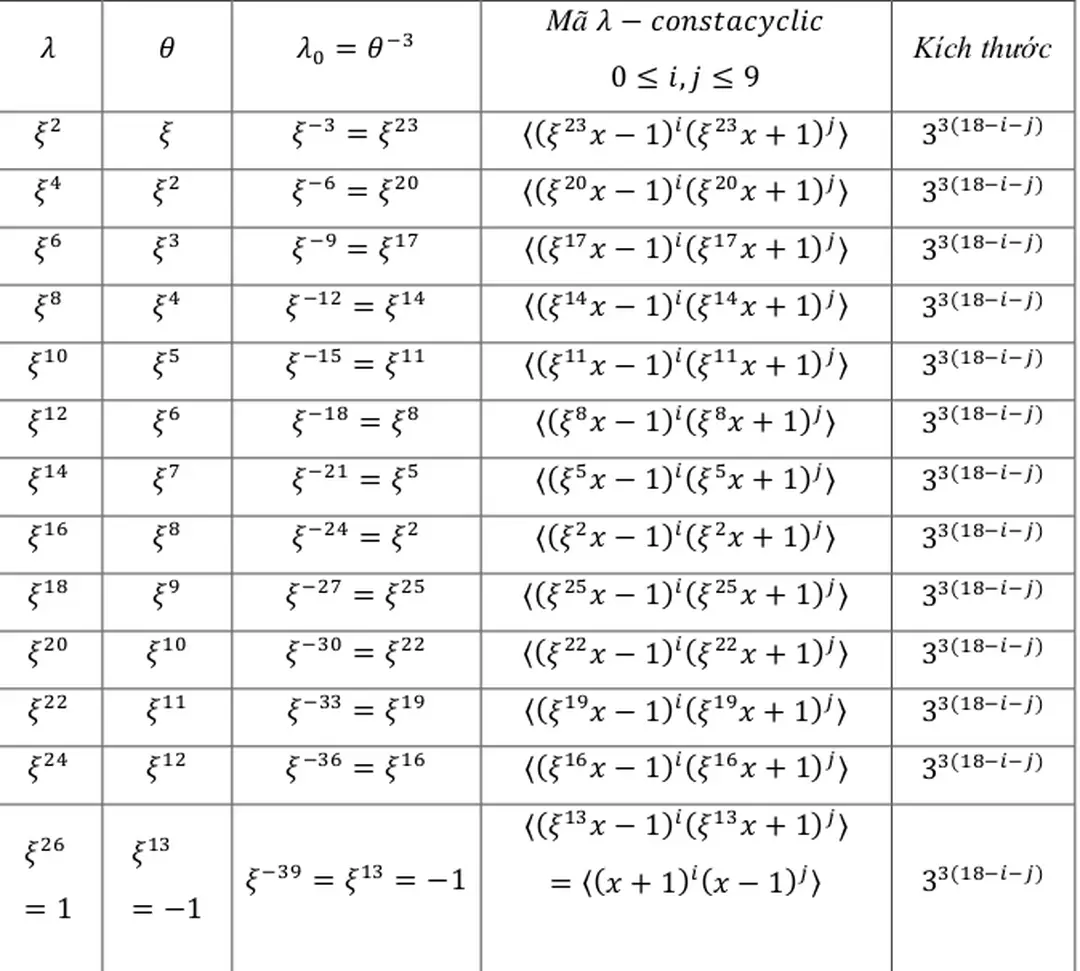
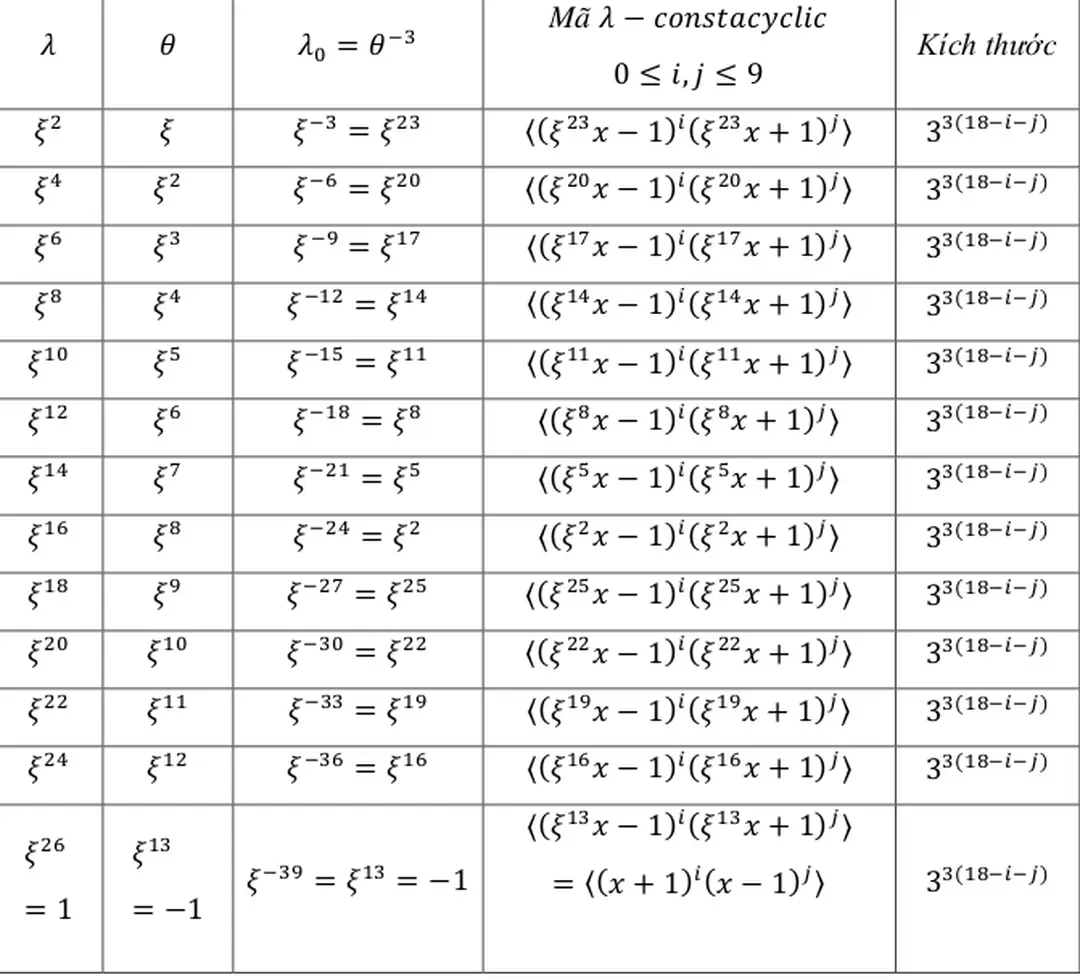
Bảng 2: Mã có độ dài 18 trên với , có nghĩa là
Vì mã có độ dài trên là iđêan của 〈 〉
〈 〉, là một vành iđêan chính, mã nhƣ vậy là 〈 〉, với
Chúng tôi tổng kết cấu trúc của tất cả mã có độ dài trên trong Bảng 1
2.2.7 Ví dụ Xét tất cả mã constacyclic có độ dài 18 trên Ở đây, và , nghĩa là chúng tôi đang làm việc trên tất cả 26 lớp mã constacyclic có độ dài trên Cho là một nghiệm của phương trình Khi đó
Thương số và số dư khi được chia cho là và (tức là
Vì vậy, giá trị của mã constacyclic được trình bày trong Bảng 2 Trong trường hợp này, cần lưu ý rằng nó có thể được biểu diễn một cách chính xác.
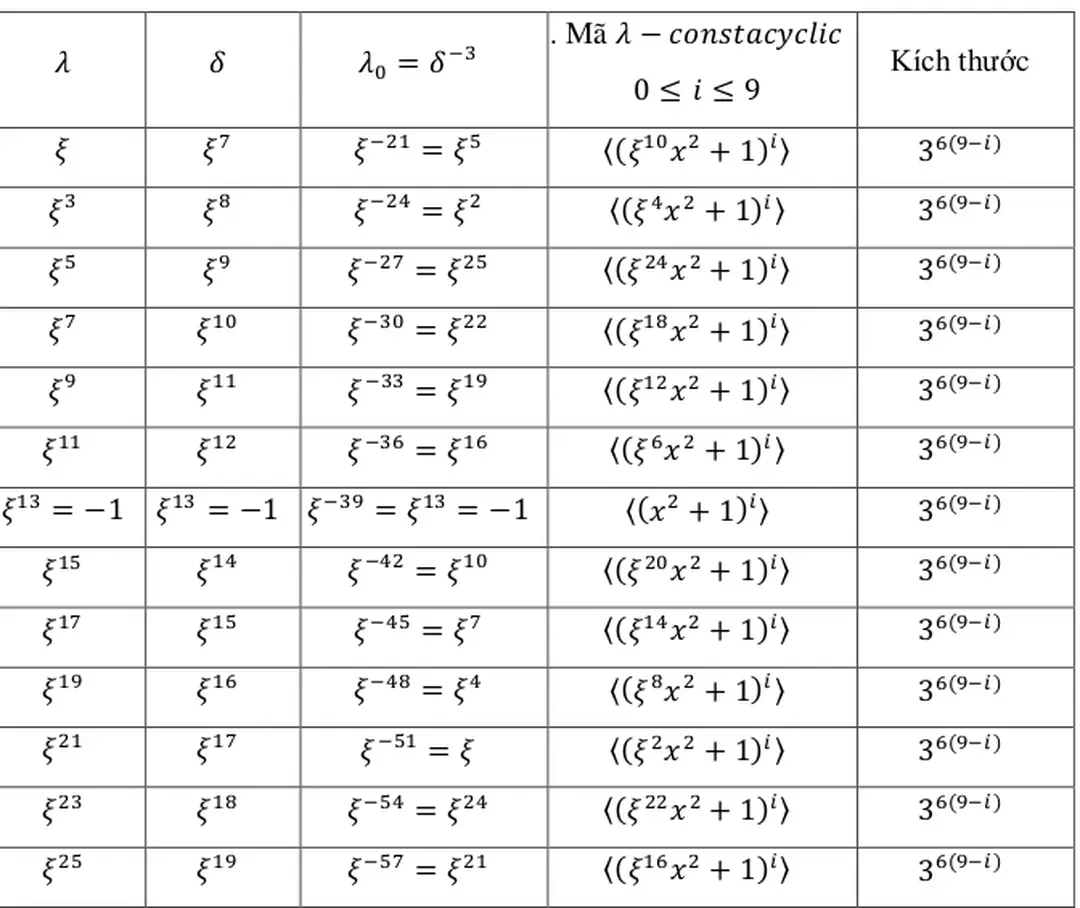
Bảng 3: Mã có độ dài 18 trên với , nghĩa là
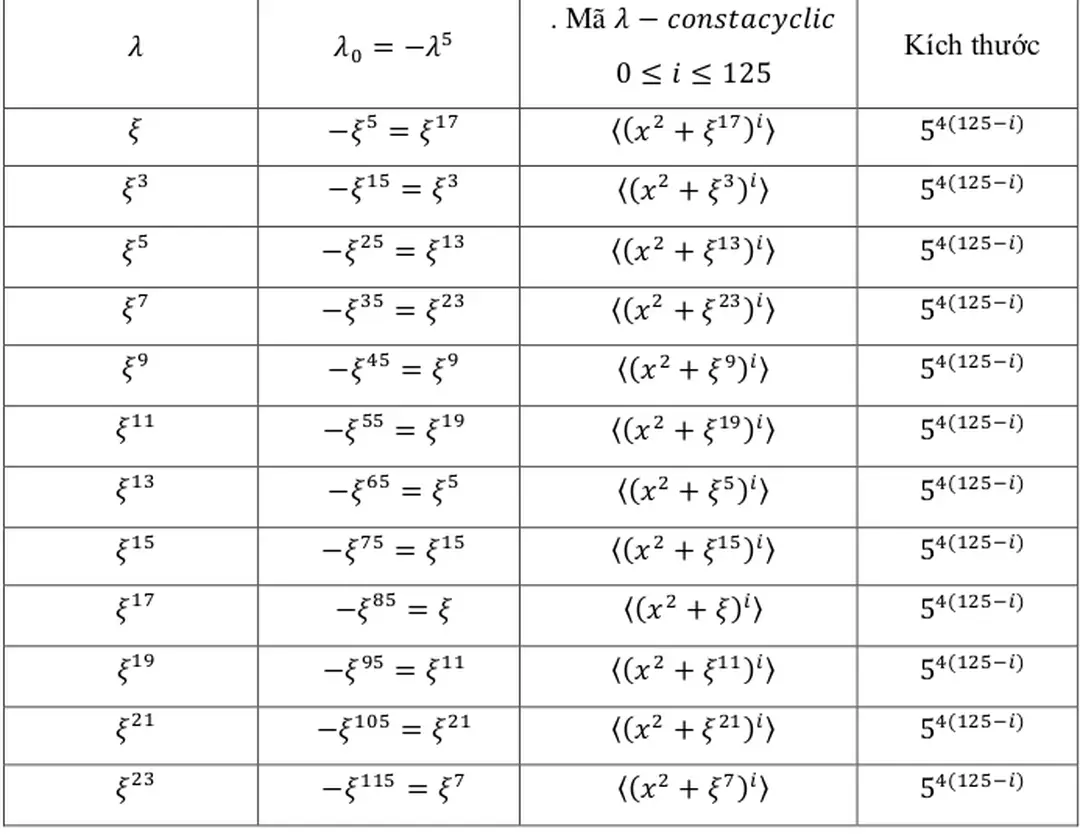
Bảng 4: Mã có độ dài 250 trên với , nghĩa là
Khi , giá trị của , và cấu trúc của mã cho bởi Bảng 3
2.2.8 Ví dụ Xét tất cả mã constacyclic có độ dài 250 trên Trong trường hợp này, và , nghĩa là chúng tôi nghiên cứu trên tất cả 24 lớp mã constacyclic có độ dài trên Cho là một nghiệm của phương trình Khi đó
Bảng 5: Mã có độ dài 250 trên với
Thương số và phần dư khi chia cho một số nguyên được xác định rõ ràng Khi giá trị thay đổi, cấu trúc mã tương ứng cũng sẽ được trình bày trong Bảng 4 Đặc biệt, trong trường hợp khác, giá trị và cấu trúc mã sẽ được minh họa trong Bảng 5.
Trong chương này, tôi trình bày tổng quan một số kết quả sau:
Bài viết này chỉ ra tính chất của một số mã, bao gồm Mệnh đề 2.1.1 và 2.1.2, đồng thời nghiên cứu về mã để trả lời câu hỏi về sự tồn tại của hai mã trong 〈 [ ] 〉 khi nào là trực giao (Mệnh đề 2.1.3) Ngoài ra, bài viết cũng xác định các điều kiện cần thiết cho sự tồn tại của mã đối ngẫu.
- Tôi nghiên cứu về tất cả các mã constacyclic có độ dài trên và liệt kê tất cả các mã có độ dài
Kết luận chương 2
Trong chương này, tôi trình bày tổng quan một số kết quả sau:
Trong bài viết này, tôi sẽ phân tích tính chất của một số mã (Mệnh đề 2.1.1 và 2.1.2) và nghiên cứu sâu về chúng để trả lời câu hỏi về sự tồn tại của mã trong 〈 [ ] 〉 trực giao (Mệnh đề 2.1.3) Bên cạnh đó, tôi cũng sẽ chỉ ra các điều kiện cần thiết để mã đối ngẫu có thể tồn tại.
- Tôi nghiên cứu về tất cả các mã constacyclic có độ dài trên và liệt kê tất cả các mã có độ dài
Một số kết quả liên quan
Cho là vành giao hoán với định nghĩa và Chúng ta ký hiệu 〈 〉 , hay 〈 〉 để đơn giản hơn, iđêan của sinh bởi phần tử , tức là 〈 〉
3.1.1 Bổ đề [12, proposition 2.2] Cho là một vành chuỗi giao hoán hữu hạn, với iđêan cực đại 〈 〉, và cho là bậc lũy linh của Khi đó:
(i) Với một số nguyên tố và số nguyên dương , | 〈 〉⁄ | trong đó ,
| | , và đặc số của ⁄〈 〉 và là lũy thừa của ;
3.1.2 Bổ đề Theo giả thiết ở đầu chương, chúng ta có
(i) , trong đó và là đơn vị của
(ii) , trong đó 〈 〉 là một nhóm con cyclic của với bậc là và | |
(iii) Với bất kỳ , gọi là bậc của Nếu thì ( )
, và nếu , khi đó với một số nguyên không âm
Phép đồng cấu vành tự nhiên 〈 〉 được xác định bởi ̅ 〈 〉 và có thể được mở rộng đến đồng cấu vành từ [ ] đến [ ] thông qua ̅ ∑ ̅̅̅, với mọi ∑ [ ] trong đó Một đa thức đơn biến [ ] được gọi là đơn biến bất khả quy cơ bản nếu ̅ là một đa thức bất khả quy.
3.1.3 Bổ đề Cho là một đa thức bất khả quy bậc trên [ ], và đặt [ ] 〈 〉 Chúng ta đồng nhất với 〈 〉 Khi đó
Vành chuỗi giao hoán hữu hạn [12, lemma 3.1] có iđêan cực đại, và [ ] 〈 ̅〉 là một trường hữu hạn với kích thước | ̅| Bậc lũy linh của trường này là , với | |
(ii) Giả sử và đặt 〈 〉 Khi đó ∏ , là đa thức tối tiểu của trên
Vì là một đa thức đơn biến bất khả quy cơ bản bậc trên, ̅ là một nghiệm của nó Do đó, ̅ cũng là một đa thức đơn biến bất khả quy bậc trên ̅, với ̅ [ ] ̅ là một nghiệm của nó.
Theo bổ đề Hensel, nếu \( p \) là một ước của \( f \) trong \( [a, b] \), thì cũng kéo theo rằng \( p \) là một ước của \( f' \) Theo (i), tồn tại một phần tử \( x \) trong \( R \) sao cho \( f(x) \equiv 0 \mod p \) Từ điều này và dựa vào Bổ đề 3.1.2 (iii), có duy nhất một số nguyên \( n \) sao cho \( f(n) \equiv 0 \mod p \).
Vì ̅ không chính phương, với mỗi , có duy nhất một nghiệm sao cho ̅ ̅ ̅ Từ | trên chúng ta kết luận
Theo Bổ đề 1.2 (iii), tồn tại một số nguyên duy nhất sao cho ̅ ̅ cùng với ̅ ̅ kéo theo Điều này dẫn đến việc các nghiệm phân biệt của trên tồn tại, từ đó ngụ ý rằng ∏.
3.1.4 Định lý Cho là một đa thức đơn biến bất khả quy bậc trong [ ], và ký hiệu [ ] 〈 〉 Với mỗi , chúng ta có những tính chất sau
(i) là lũy linh trong vành [ ] 〈 〉
(ii) [ ] 〈 〉 là một vành chuỗi hữu hạn với iđêan cực đại 〈 〉, và bậc lũy linh của là Hơn nữa, 〈 〉 〈 〉 như là iđêan của [ ] 〈 〉
(iii) ( [ ] 〈 〉)〈 〉 , là một trường hữu hạn với
(iv) [ ] 〈 〉 có iđêan: 〈 〉, Hơn nữa, chúng ta có |〈 〉| | | ,
(i) Trong vành [ ] 〈 〉, chúng ta có
Theo định lý Kummer, chúng ta nhận thấy rằng mọi ước của một số đều tồn tại Dựa vào Bổ đề 3.1.2 (i) và phương trình (1), chúng ta có thể rút ra kết luận quan trọng về các giá trị liên quan Do đó, những kết quả này khẳng định tính chính xác của lý thuyết.
(ii) Theo Bổ đề 3.1.3 tồn tại sao cho bậc của là Chúng ta kí hiệu , - dưới đây Vì , theo phương trình (1) và chúng ta có
] trong đó { }, và ∑ ∑ với Khi đó từ và , bằng phương pháp quy nạp chúng ta có thể kết luận rằng
Hiện tại, cho [ ] 〈 〉 Chúng ta nhận thấy rằng có thể được biểu diễn duy nhất dưới dạng với và , trong đó mỗi có thể được biểu diễn duy nhất dưới dạng ∑ với Đối với mỗi , hãy đặt.
∑ là một đa thức trên có bậc nhỏ hơn với hệ số trong ∑ (∑ ) [ ] 〈 〉 Khi đó
(3) Bây giờ, bởi ∑ [ ] 〈 〉 một lập luận tương tự cho thấy rằng có một đa thức đơn biến ∑ trên bậc nhỏ hơn với hệ số trong và [ ] 〈 〉 sao cho
∑ Từ điều này và phương trình (2) và phương trình (3) chúng ta suy ra
Khi đó bằng phương pháp quy nạp chúng ta có thể chứng minh rằng trong đó
Vì là phần tử lũy linh, chúng ta nhận thấy rằng 〈 〉 xảy ra khi và chỉ khi [ ] Điều này cho thấy 〈 〉 là iđêan cực đại duy nhất của [ ] Do đó, [ ] 〈 〉 được xác định là một vành chuỗi hữu hạn.
Cho là bậc lũy linh của Khi đó mọi phần tử của [ ] 〈 〉 đều có thể được biểu diễn duy nhất dưới dạng , , , có nghĩa là | [ ] 〈 〉|
Cuối cùng, vì là phần tử lũy linh và { }, ∑ là khả nghịch trong [ ] 〈 〉 Khi đó theo phương trình (2) theo đó
〈 〉 là trường hữu hạn theo (ii) và chứng minh của nó, chúng ta thấy rằng ( [ ]
(iv) Điều này suy ra ngay lập tức sau (i) – (iii) và Bổ đề 3.1.1 (iii)
Theo Bổ đề 2.1.1, mã – constacyclic có độ dài trên là iđêan của vành [ ] 〈 〉 Định lý 3.1.4 đã đƣợc chứng minh
3.1.5 Hệ quả Với bất kỳ , tất cả các mã – constacyclic phân biệt khác không có độ dài trên được cho bởi
Do đó số lƣợng mã – constacyclic có độ dài trên bằng Hơn nữa, số lƣợng từ mã trong mã – constacyclic 〈 〉 bằng
Thuộc tính cấu trúc mã – constacyclic
Trong phần này, chúng ta xem mã – constacyclic có độ dài trên với tùy ý, trong đó và
Với , tồn tại các đa thức bất khả quy cơ bản đơn biến đôi một nguyên tố cùng nhau [ ] sao cho và với Với mỗi , chúng ta kí hiệu
Vành mở rộng 〈 〉 là một vành chuỗi hữu hạn với iđêan cực đại, có bậc lũy linh bằng , và là trường hữu hạn với | | Kí hiệu 〈 〉 cho thấy rằng đa thức tối giản của trên là [ ] Dựa vào điều này và Bổ đề 3.1.3 (ii), chúng ta có thể suy ra rằng.
3.2.1 Bổ đề Chúng ta giả sử rằng thỏa mãn ( ) Khi đó
, cho là một số nguyên cố định, , sao cho
( ), tức là với một vài số nguyên
Khi , tức là , chúng ta đặt Với bất kỳ , chúng ta xác định
Khi đó là một đồng cấu vành toàn ánh từ [ ] 〈 〉 lên vành [ ] 〈 〉
Cho Vì là một thừa số của trên [ ], chúng ta có Trong vành [ ] 〈 〉, từ , , và chúng ta suy ra
Với bất kỳ [ ], xác định [ ] 〈 〉 với ( 〈 〉) Do [ ], nên là một đồng cấu vành từ [ ] đến
Từ phương trình (4), chúng ta kết luận rằng 〈 〉 là một đồng cấu vành từ 〈 〉 đến 〈 〉 Thuộc tính toàn ánh của 〈 〉 sẽ được chứng minh theo Định lý 3.2.2.
3.2.2 Định lý Trong các biểu diễn của Bổ đề 3.2.1, chúng ta xác định
[ ] 〈 〉 Khi đó là một đẳng cấu vành từ [ ] 〈 〉 vào trực tiếp vành đích [ ] 〈 〉 [ ] 〈 〉
Dựa vào chứng minh của Bổ đề 3.2.1, chúng ta có thể kết luận rằng đồng cấu vành từ [ ] 〈 〉 đến [ ] 〈 〉 [ ] 〈 〉 tồn tại Giả sử có [ ], thì sẽ có một ma trận duy nhất ( ) thỏa mãn ( ) Với mỗi , từ , trong [ ] 〈 〉 và thông qua việc tính toán ma trận, chúng ta có thể suy ra kết quả cần thiết.
Trong bài viết này, chúng ta xem xét một ma trận khả nghịch trong mỗi vành [ ] 〈 〉 Giả sử có một nghiệm của phương trình trong một số vành mở rộng của Theo Bổ đề 3.1.3 (ii), điều này dẫn đến { } , -.
Khi xem xét tự đẳng cấu Frobenius trong không gian [ ] 〈 〉, chúng ta giả sử có một ma trận khả nghịch Từ đó, chúng ta có thể rút ra rằng ma trận này là đơn ánh Hơn nữa, áp dụng Định lý 3.1.4 với ∑, chúng ta có thể khẳng định được các tính chất quan trọng liên quan đến ma trận trong không gian này.
Do đó là một song ánh Vì vậy, là toàn ánh với mọi
Với bất kỳ cố định, chúng ta có ( ) theo Bổ đề 3.1.2 (iii) Dưới đây, chúng ta kí hiệu
[ ] 〈 〉, và [ ] 〈 〉 với Khi đó theo Định lý 3.2.2 suy ra rằng
3.2.3 Bổ đề Cho Trong sự trình bày của Bổ đề 3.2.1 chúng ta có
(i) ( ) là một đơn vị của vành với bất kỳ ,
Trong đó 〈 〉 là iđêan của được tạo bởi và
〈 〉 là iđêan của được tạo bởi ( )
Cho là một nghiệm của phương trình trong vành mở rộng Theo Bổ đề 3.1.3 (ii), ta có { } , - Giả sử rằng , với và
(i) Từ ∏ ( ) ∏ ( ), chúng ta suy ra
Trong bài viết này, chúng ta xem xét một đơn vị trong vành, cụ thể là ( ) ∏ ( ) ∏ [ ( )] Đối với bất kỳ , theo định lý 3.1.4, chúng ta xác định rằng nếu có một phần tử lũy linh trong , thì cũng có phần tử lũy linh trong Do đó, ( ) là một đơn vị trong với mọi , và từ đó suy ra rằng ( ) là một đơn vị của vành.
(ii) Từ chúng ta suy ra
[ ] trong Với theo đó ∏ ( ) , nó có nghĩa là ( ) , với [∏ ( )] là một đơn vị của theo (i) Do đó 〈 ( )〉 〈 〉 là một iđêan của
(iii) Vì là một đồng cấu vành toàn ánh từ lên , theo phép chứng minh của (ii) theo đó (〈 〉 ) 〈 ( )〉 〈[ ( )]〉
(i) Tất cả mã – constacyclic phân biệt có độ dài trên được cho bởi
Do đó số lượng mã – constacyclic có độ dài trên bằng (ii) là vành chính
(iii) Theo sự biểu diễn ở phần (i), chúng ta có | | ∑ ( )
(i) Với mỗi , theo Định lý 3.1.4 tất cả iđêan phân biệt của vành đƣợc cho bởi 〈 〉 , Khi đó từ chúng ta suy ra số lƣợng iđêan của vành là
Với bất kỳ và , chúng ta ký hiệu 〈 〉 và 〈 〉 Với bất kỳ , từ Bổ đề 3.2.3 chúng ta suy ra rằng
Tương tự, ta có 〈 〉 với bất kỳ Bây giờ, nếu , khi đó 〈 〉 〈 〉 kéo theo , với mọi
Nhƣ đã nêu ở trên, chúng ta kết luận rằng
〈 〉 , với và , là tất cả iđêan phân biệt của
(ii) Điều này đƣợc suy ra từ (i)
(iii) Theo Định lý 3.2.2 và phép chứng minh của (i), ta có
Khi đó theo Định lý 3.1.4 (iv) chúng ta suy ra rằng | | ∏ | 〈 〉 | ∏ ( ) ∑ ( )
Mã đối ngẫu của mã – constacyclic
Trong phần này, chúng ta xem xét các mã đối ngẫu của mã – constacyclic có độ dài trên cho bất kỳ không đổi Từ [11, Proposition 3.1.4] chúng ta suy ra
3.3.1 Bổ đề Mã đối ngẫu của mã – constacyclic có độ dài trên là một mã – constacyclic có độ dài trên Nói cách khác, đối ngẫu của một iđêan của vành [ ] 〈 〉 là một iđêan của vành [ ] 〈 〉
Theo sự trình bày trong phần 2, cho là đa thức tối giản của trên Khi đó có một phần tử duy nhất sao cho với mỗi , và
Rõ ràng là [ ] 〈 〉 [ ] 〈 〉 [ ] [ ] Theo dưới đây, chúng biểu thị ̂ [ ] 〈 〉, ̂ [ ] 〈 〉,
Vì , trong đó , theo Định lý 3.2.2 ta có ̂ ̂ ̂ Từ điều này và bằng sự chứng minh tương tự Bổ đề 3.2.3 và Định lý 3.2.4, chúng ta suy luận
(i) Tất cả mã – constacyclic phân biệt có độ dài trên được cho bởi ̂ 〈 〉 ̂ , ,
Do đó số lượng của mã – constacyclic có độ dài trên là
(ii) ̂ là một vành chính
(iii) Theo sự biểu diễn của (i), chúng ta có | ̂ | ∑ ( ) Đối với mã đối ngẫu của mã – constacyclic có độ dài trên , chúng ta có
3.3.3 Định lý Theo sự biểu diễn của Định lý 3.2.4 và Hệ quả 3.3.2, chúng ta có ̂ ( ) , ,
Theo Định lý 3.2.4, một iđêan được sinh ra từ một tập hợp cho trước Khi đó, iđêan và ̂ ( ) được xác định bởi Các phép chia Euclidean của và theo là [ ] và [ ].
Theo Định lý 3.1.4 và chứng minh Bổ đề 3.2.3 (ii), chúng ta có thể suy ra rằng ( ) ( ) trong với mọi Kết luận này dẫn đến việc ( ) ( ( ) ( )) Vì là một vành đẳng cấu theo Định lý 3.2.2, chúng ta xác định rằng trong , có nghĩa là ( ) trong [ ] Do đó, [ ( )][ ( )] ( ) trong [ ] Từ điều này, chúng ta suy ra rằng
Hơn nữa, nếu ( ) , chúng ta có , và do đó ⃖ ⃖ ( ) ( ) * ( ) ( )+ ( ) trong ̂ Nếu không, cho ( ) Từ trong ̂ , chúng ta suy ra ⃖ 0 ( ) ( ) ( ) /1 trong ̂
Vì là một đơn vị của ̂ , chúng ta có
| | (theo Định lý 3.2.4 và Hệ quả 3.3.2), chúng ta kết luận rằng ̂ ( )
Với mã constacyclic tự đối ngẫu trên vành chuỗi hữu hạn chúng ra có những điều sau đây
3.3.4 Hệ quả Với mọi số lẻ và số nguyên dương , cho
, với là các đa thức bất khả quy đơn biến phân biệt trên trường thỏa mãn
, ; , , với nào đó Cho Khi đó:
(i) Tất cả mã tự đối ngẫu – constacyclic có độ dài trên được cho bởi
(ii) Số lượng mã tự đối ngẫu – constacyclic có độ dài trên là
(iii) Nếu , khi đó 〈 〉 là mã tự đối ngẫu – constacyclic có độ dài duy nhất trên
Rõ ràng là Cho là một mã – constacyclic có độ dài duy nhất trên Theo Định lý 3.2.4 có một bộ giá trị ( ) gồm các số nguyên , , sao cho
〈 〉 Từ điều này và theo Định lý 3.3.3 chúng ta suy ra
Do đó, là tự đối ngẫu khi và chỉ khi
{ Điều này tương đương với , với mọi , và
Nếu , khi đó mã tự đối ngẫu – constacyclic có độ dài duy nhất trên đƣợc cho bởi 〈( ) 〉 〈 〉
Nhận xét Khi và , mã – constacyclic và mã đối ngẫu của chúng có độ dài trên đã đƣợc khảo sát (xem Theorem 3.3, Theorem 3.4 và Corollary 3.5 trong [19])
Cho một vành Galois đặc trưng, có thể thấy rằng điều kiện xảy ra khi và chỉ khi một số nhất định tồn tại Theo Định lý 3.3.3, từ đó chúng ta có thể suy ra một kết luận quan trọng.
3.3.5 Hệ quả Cho , lẻ và Chúng ta giả sử
, với là các đa thức bất khả quy đơn biến đôi một nguyên tố cùng nhau trên thỏa mãn
, ; , , với nào đó Cho nếu , và và với một số nếu Khi đó:
(i) Tất cả mã tự đối ngẫu của mã – constacyclic độ dài trên được cho bởi
Số lượng mã tự đối ngẫu của mã constacyclic có độ dài nhất định là một yếu tố quan trọng Đặc biệt, mã tự đối ngẫu duy nhất của mã constacyclic với độ dài này được xác định khi thỏa mãn một điều kiện cụ thể.
(iii) Nếu là chẵn và , 〈 〉 ( [ ] 〈 〉) là mã tự đối ngẫu duy nhất của mã – constacyclic độ dài trên
Chúng ta chỉ cần chứng minh kết luận (iii) Cho Khi đó 〈 〉 là mã tự đối ngẫu duy nhất của mã – constacyclic độ dài trên Theo
Bổ đề 3.2.3 (ii) và Định lý 3.1.4 (ii) ta có
[ ] 〈 〉 là iđêan của [ ] 〈 〉 sinh bởi , với mọi Do đó,
Nhận xét Đặt trong Hệ quả 3.3.5 Người ta có thể thu được kết quả cho mã negacyclic có độ dài tùy ý trên vành Galois
Trong trường hợp đặc biệt, theo Định lý 3.1.4 (ii), chúng ta có thể xác định một số phần tử khả nghịch của vành [ ] 〈 〉, dẫn đến việc suy ra * + Do đó, vì là phần tử khả nghịch của [ ] 〈 〉, chúng ta có thể kết luận rằng.
The results for the negacyclic code of the specified length can be deduced from Corollary 3.1.5 and Corollary 3.3.5, as referenced in [8, Proposition 3.2, Proposition 3.3, Theorem 3.4, Theorem 3.6, Corollary 3.7].
3.3.6 Ví dụ Xem xét mã – constacyclic có độ dài trên [ ] Đầu tiên, chúng ta có , trong đó
, , là các đa thức bất khả quy cơ bản đơn biến đôi một nguyên tố cùng nhau trong [ ] và thỏa mãn , , và Theo và Định lý 3.3.5 ta có:
(i) Có mã – constacyclic có độ dài phân biệt trên , nghĩa là iđêan của vành [ ] 〈 〉 〈 〉, (ii) 〈 〉 cũng là một mã – constacyclic có độ dài trên
(iii) Có mã tự đối ngẫu của mã – constacyclic có độ dài trên :
Kết luận chương 3
Trong chương này, tôi trình bày tổng quan một số kết quả sau:
- Đƣa ra các thuộc tính cấu trúc mã – constacyclic có độ dài tùy ý trên với bất kỳ
- Cung cấp mã tự đối ngẫu trên vành chuỗi hữu hạn và vành Galois
- Khoảng cách Hamming của mã – constacyclic trên vành chuỗi hữu hạn là một chủ đề thú vị trong tương lai
KẾT LUẬN CHUNG VÀ KIẾN NGHỊ
Nghiên cứu này tập trung vào mã trên trường hữu hạn, đặc biệt là mã constacyclic với độ dài trường, cùng với mã và mã đối ngẫu của chúng trên vành chuỗi hữu hạn Các kết quả đạt được từ khóa luận tốt nghiệp này cung cấp cái nhìn tổng quan về các kết quả liên quan đến lĩnh vực này.
1 Chỉ ra các tính chất cơ bản của trường , phân loại các phần tử khả nghịch của nó; Mô tả cấu trúc mã ; Tính toán các đại lƣợng nhƣ số lƣợng từ mã, mã đối ngẫu cùng điều kiện để tồn tại mã tự đối ngẫu, công thức xác định khoảng cách Hamming
2 Chỉ ra cấu trúc mã độ dài , đồng thời tính toán số các từ mã và mô tả mã đối ngẫu
3 Chỉ ta thuộc tính cấu trúc mã , mã đối ngẫu của nó trên vành chuỗi hữu hạn
Trong thời gian tới, tôi mong muốn tiếp tục nghiên cứu các vấn đề sau:
1 Nghiên cứu mã độ dài trên trường hữu hạn, cụ thể là trường và mã và có độ dài trên trường
2 Tiếp tục chỉ ra các tính chất của mã constacyclic và tính toán các đại lƣợng liên quan nhƣ khoảng cách Hamming, lƣợng Hamming
3 Tiếp tục nghiên cứu về điều kiện để mỗi mã tuyến tính là mã constacyclic nghiệm bội.